Exercise 1
Consider the following boundary-value problem:
\[\begin{split}
\begin{array}{rl}
-\epsilon u'' + x u' + u = 1, & x \in \Omega = [0, 1] \\
u(0) = 1, & \\
u'(1) = 7, &
\end{array}
\end{split}\]
where \(\epsilon > 0\) is a constant.
a) Derive a weak form of the problem, with appropriate spaces.
Solution: We multiply the PDE by a sufficiently smooth test function \(v\) and integrate, using the integration-by-parts formula:
\[\begin{split}
\begin{aligned}
(v, 1) &= -\epsilon(v, u'') + (v, xu') + (v,u) = [IBP] \\
&= \left. -\epsilon v u' \right|_{0}^{1} + \epsilon(v', u') + (v, xu') + (v,u). \\
\end{aligned}
\end{split}\]
Since we have a Dirichlet condition at the left boundary, we may impose a Dirichlet condition on the test function at that boundary as well. We are free to choose the boundary value, so for simplicity we choose the homogeneous Dirichlet BC \(v(0)=0\) so that the boundary terms vanish at \(x=0\). We obtain
\[\begin{split}
\begin{aligned}
(v, 1) &= -\epsilon v(1) u'(1) + \epsilon(v', u') + (v, xu') + (v,u) \\
&= -7\epsilon v(1) + \epsilon(v', u') + (v, xu') + (v,u),
\end{aligned}
\end{split}\]
where we used the BC \(u'(1) = 7\). We need \(u\), \(u'\), \(v\), and \(v'\) to be integrable, so we define the spaces
\[\begin{split}
\begin{aligned}
V_0 &:= \left\{v: \lVert v \rVert < \infty, \lVert v' \rVert < \infty, v(0)=0 \right\}, \\
V_1 &:= \left\{v: \lVert v \rVert < \infty, \lVert v' \rVert < \infty, v(0)=1 \right\}.
\end{aligned}
\end{split}\]
The weak form reads: Find \(u\in V_1\) such that
\[
\epsilon(v', u') + (v, xu') + (v,u) = (v,1) + 7\epsilon v(1) \quad \forall v\in V_0.
\]
b) Explain the difference between test and trial spaces in general. What are the test/trial spaces in a)?
Solution: We look for a solution in the trial space. The solution has to satisfy the weak form for all functions in the test space. In this particular example, the trial space is \(V_1\) and the test space is \(V_0\). They differ only in the prescribed value at the left boundary, where we have an inhomogeneous Dirichlet BC for \(u\).
c) Sketch the five “hat functions” that form a basis for the space of piecewise linear functions on a mesh of four subintervals of equal length.
Solution:
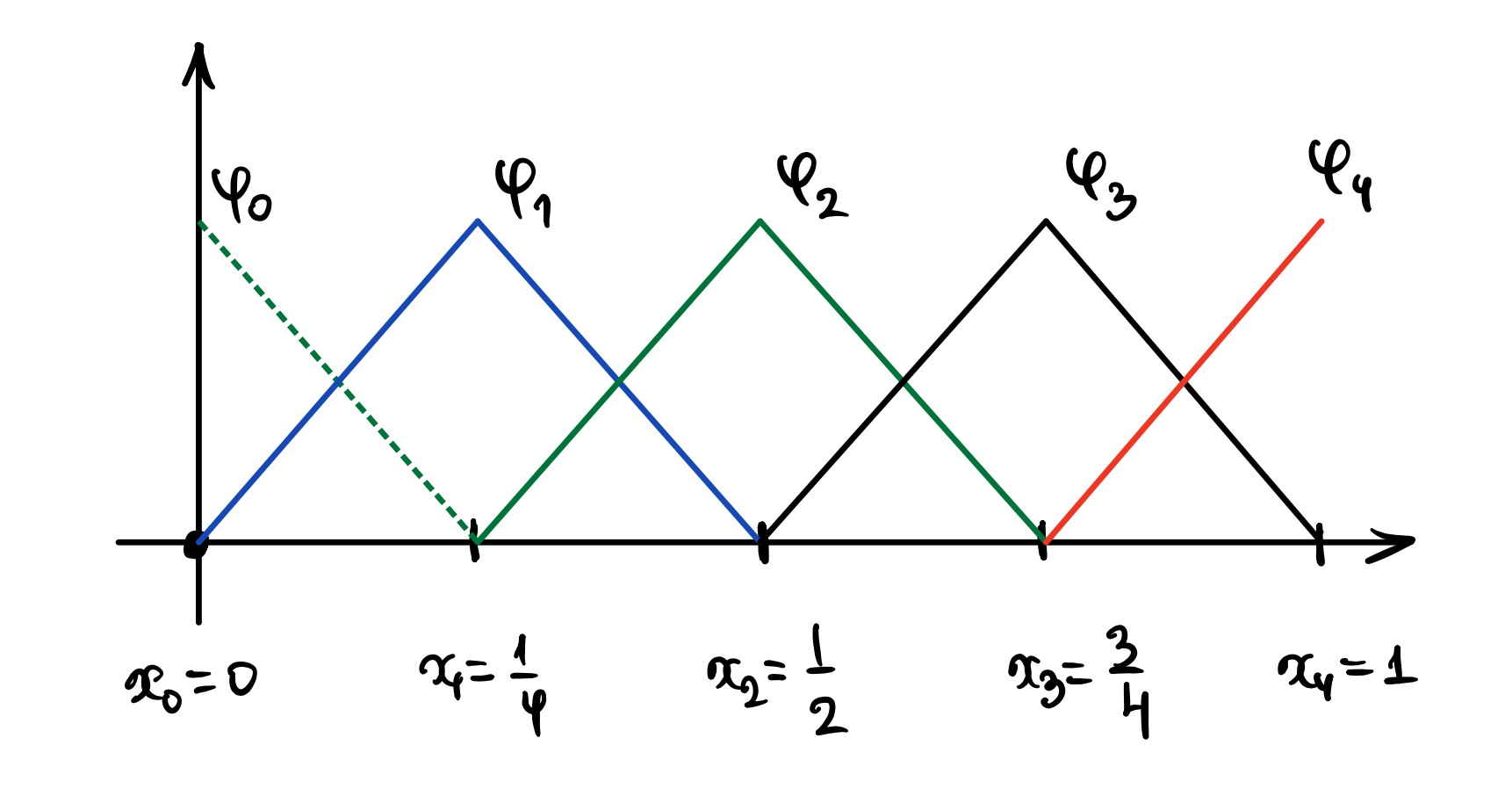
d) The hat function \(\varphi_1\) satisfies \(\varphi_1(0.25) = 1\). How does \(\varphi_1\) depend on \(x\)? Write down the mathematical expression.
Solution:
In general, we have
\[\begin{split}
\varphi_i(x) = \left\{
\begin{array}{ll}
\displaystyle
\frac{x-x_{i-1}}{x_i-x_{i-1}}, &x \in [x_{i-1}, x_i] \\
\displaystyle
\frac{x_{i+1}-x}{x_{i+1}-x_i}, &x \in (x_{i-1}, x_i] \\
0 &\mbox{otherwise}
\end{array}
\right.
\end{split}\]
Here we have \(i=1\), \(x_i=x_1=0.25\), \(x_{i-1}=0\), and \(x_{i+1}=0.5\), which yields
\[\begin{split}
\varphi_1(x) = \left\{
\begin{array}{ll}
\displaystyle
\frac{x-0}{0.25} = 4x, &x \in [0, 0.25] \\
\displaystyle
\frac{0.5-x}{0.25} = 2-4x, &x \in (0.25, 0.5] \\
0 &\mbox{otherwise}
\end{array}
\right.
\end{split}\]
e) For the mesh of four equal subintervals, formulate the finite element method and derive the corresponding linear system of equations. You do not need to evaluate any of the integrals that appear in the stiffness matrix and load vector.
Solution:
We define the following spaces of continuous, piecewise linear functions that satisfy Dirichlet conditions at \(x=0\):
\[\begin{split}
\begin{aligned}
V_{h,0} &= \left\{v: v \in C_0(0,1), \; v|_{I_i}\in P_1(I_i), \; i=1,2,3,4, \; v(0) = 0 \right\}, \\
V_{h,1} &= \left\{v: v \in C_0(0,1), \; v|_{I_i}\in P_1(I_i), \; i=1,2,3,4, \; v(0) = 1 \right\}.
\end{aligned}
\end{split}\]
We obtain the finite element method by replacing the spaces in the weak form by the corresponding spaces of piecewise linear functions:
Find \(u_h \in V_{h,1}\) such that
\[
\epsilon(v', {u_{h}}') + (v, x{u_{h}}') + (v,u_h) = (v,1) + 7\epsilon v(1) \quad \forall v \in V_{h,0}.
\]
Since \(v \in V_{h,0}\), it can be expressed as a linear combination of \(\varphi_1-\varphi_4\):
\[
v = \sum \limits_{i=1}^4 \alpha_i \varphi_i .
\]
If the FEM equation is satisfied for each hat function separately, then it is also satisfied for any linear combination of hat functions and thus for any \(v\in V_{h,0}\). We seek \(u_h \in V_{h,1}\) such that
\[
\underbrace{\epsilon({\varphi_i}', {u_{h}}')}_{T_1} + \underbrace{(\varphi_i, x{u_{h}}')}_{T_2} + \underbrace{(\varphi_i,u_h)}_{T_3} = (\varphi_i,1) + 7\epsilon \varphi_i(1) \quad i = 1,2,3,4.
\]
Since \(u_h \in V_{h,1}\), it can be written as
\[
u_h = 1\cdot \varphi_0 + \sum \limits_{j=1}^4 \xi_j \varphi_j,
\]
for some unknown coefficients \(\xi_j\). Inserting this ansatz in the equation above yields
\[
T_1 = \epsilon({\varphi_i}',{\varphi_0}') + \sum \limits_{j=1}^4 \epsilon({\varphi_i}', {\varphi_j}') \xi_j,
\]
\[
T_2 = ({\varphi_i},x{\varphi_0}') + \sum \limits_{j=1}^4 ({\varphi_i}, x {\varphi_j}') \xi_j,
\]
\[
T_3 = (\varphi_i,\varphi_0) + \sum \limits_{j=1}^4 (\varphi_i,\varphi_j) \xi_j.
\]
After moving all known terms (terms that do not contain \(\xi_j\)) to the right-hand-side, we obtain the system of equations
\[
A \xi = b,
\]
where
\[
A_{ij} = \epsilon({\varphi_i}', {\varphi_j}') + ({\varphi_i}, x {\varphi_j}') + (\varphi_i,\varphi_j),
\]
\[
b_i = (\varphi_i,1) + 7\epsilon \varphi_i(1) - \epsilon({\varphi_i}',{\varphi_0}') - ({\varphi_i},x{\varphi_0}') - (\varphi_i,\varphi_0) .
\]
To further simplify the load vector \(b\), note that
\[\begin{split}
7\epsilon\varphi_i(1) = \left\{
\begin{array}{ll}
0, & i \neq 4, \\
7\epsilon, & i = 4,
\end{array}
\right.
\end{split}\]
\[\begin{split}
\epsilon({\varphi_i}',{\varphi_0}') = \left\{
\begin{array}{ll}
\epsilon({\varphi_1}',{\varphi_0}'), & i = 1, \\
0, & i > 1,
\end{array}
\right.
\end{split}\]
\[\begin{split}
({\varphi_i},x{\varphi_0}') = \left\{
\begin{array}{ll}
({\varphi_1},x{\varphi_0}'), & i = 1, \\
0, & i > 1,
\end{array}
\right.
\end{split}\]
\[\begin{split}
(\varphi_i,\varphi_0) = \left\{
\begin{array}{ll}
(\varphi_1,\varphi_0), & i = 1, \\
0, & i > 1.
\end{array}
\right.
\end{split}\]
Hence, we have
\[\begin{split}
b =
\begin{bmatrix}
(\varphi_1,1) - \epsilon({\varphi_1}',{\varphi_0}') - ({\varphi_1},x{\varphi_0}') - (\varphi_1,\varphi_0)\\
(\varphi_2,1)\\
(\varphi_3,1)\\
(\varphi_4,1) + 7\epsilon
\end{bmatrix}.
\end{split}\]
