Problem set 2: Finite difference methods#

Topics covered: Finite difference methods, boundary condition enforcement, stability.

Note: If you miss the problem solving class, you have to submit solutions to 1a)-d) and 2a)-b) in Studium before the deadline.

Preliminaries#

Consider a uniform grid of \(m+1\) points, with grid spacing \(h = \frac{L}{m}\). Let \(\mathbf{e}_{\ell}\) and \(\mathbf{e}_r\) denote the following vectors in \(\mathbb{R}^{m+1}\):

\[\begin{split} \mathbf{e}_{\ell} = \begin{bmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix}, \quad \mathbf{e}_{r} = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 1 \end{bmatrix}. \end{split}\]

Definition of \(D_1\)#

A difference operator \(D_1\) is a first-derivative SBP operator with quadrature matrix \(H\) if \(H=H^T>0\) and

\[ HD_1 = \mathbf{e}_r \mathbf{e}_r^T - \mathbf{e}_\ell \mathbf{e}_\ell^T - D_1^T H . \]

Definition of \(D_2\)#

A difference operator \(D_2\) approximating \(\partial^2/\partial\,x^2\) is a second-derivative SBP operator if

\[ HD_2 = \mathbf{e}_r \mathbf{d}_r^T - \mathbf{e}_{\ell} \mathbf{d}_\ell^T - M, \]

where \(H=H^T>0\), \(M=M^T \ge 0\), and \(\mathbf{d}_\ell^T v\simeq u_x|_{x=0}\), \(\mathbf{d}_r^T v \simeq u_x |_{x=L}\) are finite difference approximations of the first derivatives at the left and right boundary points.

Discrete inner product#

Let \((\cdot, \cdot)_H\) denote the discrete inner product, defined by

\[ (\mathbf{u}, \mathbf{v})_H = \mathbf{u}^* H \mathbf{v}. \]

Note that \((\cdot, \cdot)_H\) approximates the \(L^2\) inner product \((\cdot, \cdot)\), since \(H\) is a quadrature operator. In the discrete inner product, the SBP operators satisfy

\[ (\mathbf{u}, D_1 \mathbf{v})_H = (\mathbf{e}_r^T \mathbf{u})^* (\mathbf{e}_r^T \mathbf{v}) - (\mathbf{e}_\ell^T \mathbf{u})^* (\mathbf{e}_\ell^T \mathbf{v}) - (D_1 \mathbf{u}, \mathbf{v})_H \]

and

\[ (\mathbf{u}, D_2 \mathbf{v})_H = (\mathbf{e}_r^T \mathbf{u})^* (\mathbf{d}_r^T \mathbf{v}) - (\mathbf{e}_\ell^T \mathbf{u})^* (\mathbf{d}_\ell^T \mathbf{v}) - \mathbf{u}^* M \mathbf{v}. \]

Note the similiarties with the corresponding integration-by-parts formulas.

Stability regions of Runge–Kutta methods#

The figure below shows the stability regions for three different Runge–Kutta methods. Here \(k\) denotes the time step and \(\lambda\) the coefficient in the test equation:

\[ y' = \lambda y \]
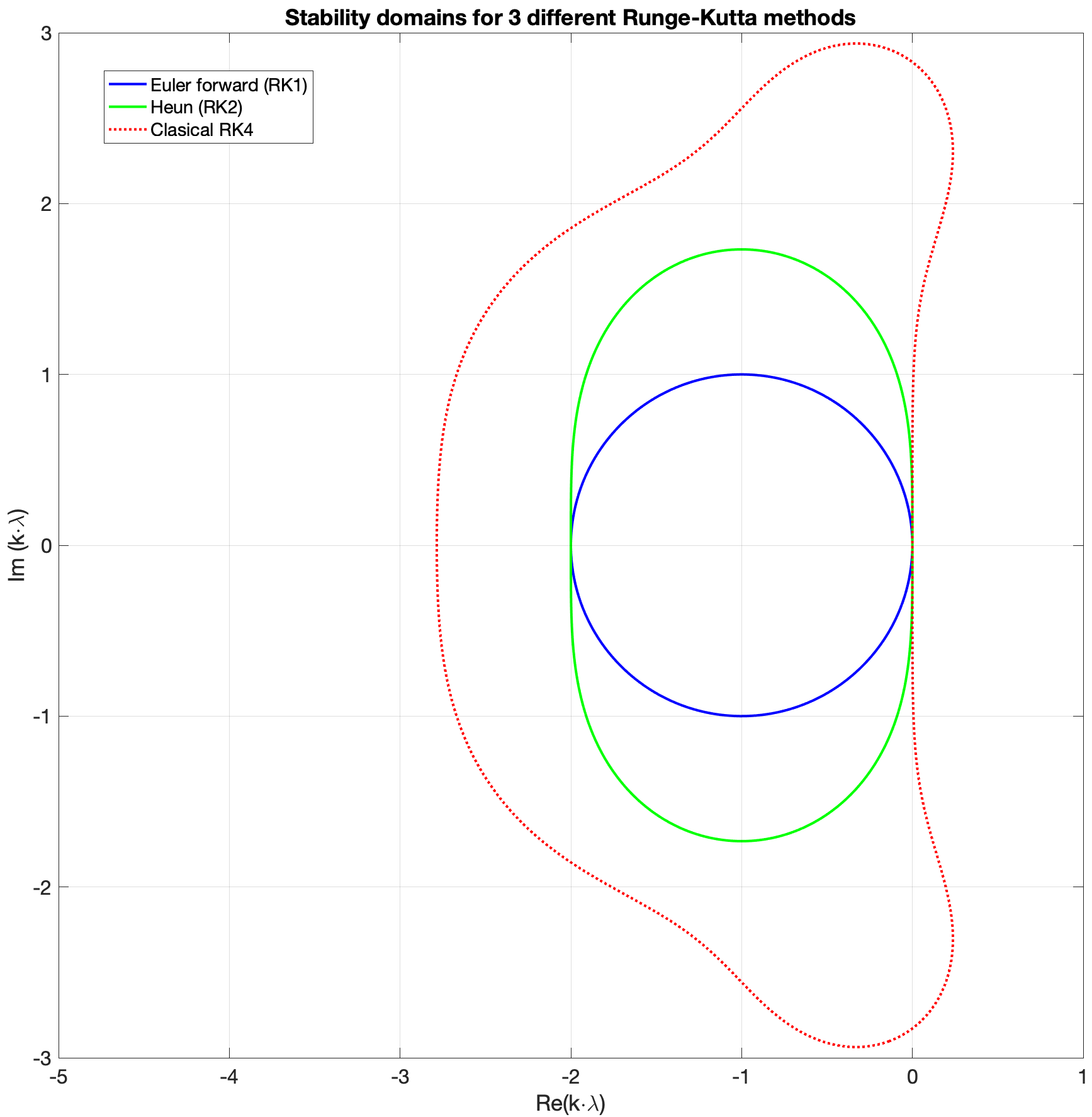
../../_images/Stability_Domain.png

Exercise 1#

Consider the advection-diffusion IBVP,

\[\begin{split} \begin{array}{lll} u_t=au_{x} +bu_{xx}, & 0 < x < L, & t> 0,\\ au+2bu_x=0, &x=0,& t > 0,\\ au+2bu_x=0, &x=L,& t > 0,\\ u=f,& 0\le x \le L, & t= 0,\\ \end{array} \end{split}\]

where \(a\) and \(b>0\) are real constants. You may assume that \(u\) is real too.

a) Prove that the finite difference operator \(D_+D_-\) (obtained by stacking \(D_+\) and \(D_-\)) is a second-order approximation of \(\partial^2/\partial x^2\). The operator is given by

\[ (D_+D_-\mathbf{v})_j = \frac{v_{j-1} - 2v_j + v_{j+1}}{h^2}. \]

b) Use the energy method to show that the IBVP is well posed.

c) Derive a stable semi-discrete SBP-SAT approximation of the IBVP.

d) Consider using RK4 for time-integration. Approximately how does the largest stable time step depend on the grid spacing \(h\)? Hint: How do the largest eigenvalues of \(D_1\) and \(D_2\) depend on \(h\)?

Exercise 2#

Consider the following problem,

\[\begin{split} \begin{array}{rll} {\bf u}_{t}= A{\bf u}_x & 0 < x < L , & t > 0,\\ u^{(1)}=0 , &x=0,& t > 0,\\ u^{(1)}+u^{(2)}=0, &x=L,& t > 0,\\ {\bf u}={\bf f},& 0 \le x \le L, & t= 0,\\ \end{array} \end{split}\]

where \({\bf f}={\bf f}(x)\) is the initial data and

\[\begin{split} {\bf u}=\begin{bmatrix} u^{(1)}\\ u^{(2)}\\ \end{bmatrix}, \quad A=\begin{bmatrix} 2&1 \\ 1&0\\ \end{bmatrix}\;. \end{split}\]

a) Use the energy method to show that the IBVP is well posed. You may assume that the solution is real.

b) Explain why Euler forward (RK1) is not a suitable time-integrator for this IBVP. Hint: Ignore the boundary conditions and study the periodic problem. What are the eigenvalues of the matrix that discretizes the right-hand side? You might also want to study the ODEs that the Fourier coefficients satisfy.

c) Derive a stable SBP-SAT approximation of the IBVP.

Hint: For a system of equations it is useful to extend all operators to 2 components. We will use the bar notation for extended operators. We define

\[\begin{split} \begin{aligned} \bar{D}_1 &= I_2 \otimes D_1, \quad \bar{H} = I_2 \otimes H, \\ \bar{\mathbf{e}}_\ell &= I_2 \otimes \mathbf{e}_{\ell}, \quad \bar{\mathbf{e}}_r = I_2 \otimes \mathbf{e}_{r}, \end{aligned} \end{split}\]

where \(I_n\) denotes the \(n\times n\) identity matrix. We also extend the coefficient matrix \(A\) to an \((m+1)\)-point grid:

\[ \bar{A} = A \otimes I_{m+1}. \]

The SBP property translates to the following property for the extended operators:

\[\begin{split} \begin{aligned} (\mathbf{u}, \bar{A} \bar{D}_1 \mathbf{v})_\bar{H} &= (\bar{\mathbf{e}}_r^T \mathbf{u})^* A (\bar{\mathbf{e}}_r^T \mathbf{v}) - (\bar{\mathbf{e}}_\ell^T \mathbf{u})^* A (\bar{\mathbf{e}}_\ell^T \mathbf{v}) \\ &- (\bar{D}_1 \mathbf{u}, \bar{A} \mathbf{v})_{\bar{H}} \end{aligned} \end{split}\]