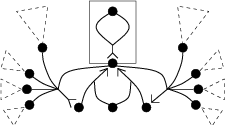
Solo Diagrams

Cosimo Laneve, Joachim Parrow, and Björn Victor

Abstract:

We address the problems of implementing the replication operator efficiently in the solos calculus---a calculus of mobile processes without prefix. This calculus is expressive enough to admit an encoding of the whole fusion calculus and thus the pi-calculus.

We show that nested occurrences of replication can be avoided, that the size of replicated terms can be limited to three particles, and that the usual unfolding semantics of replication can be replaced by three simple reduction rules. To illustrate the results and show how the calculus can be efficiently implemented we present a graphic representation of agents in the solos calculus, adapting ideas from interaction diagrams and pi-nets.

In N. Kobayashi and B.C. Pierce, eds, Proceedings of TACS 2001, Sendai, Japan, volume 2215 of Lecture Notes in Computer Science, pages 127-144. Springer-Verlag, 2001. (Postscript, compressed, PDF) [Copyright © Springer-Verlag.]

If you have a Flash plugin, you can see my presentation at TACS 2001.

See also these related papers:

The Fusion Calculus: Expressiveness and Symmetry in Mobile Processes, by Joachim Parrow and Björn Victor, LICS'98.
Concurrent Constraints in the Fusion Calculus, by Björn Victor and Joachim Parrow, ICALP'98.
The Tau-Laws of Fusion, by Joachim Parrow and Björn Victor, CONCUR'98.
The Fusion Calculus: Expressiveness and Symmetry in Mobile Processes, PhD thesis by Björn Victor.
Symbolic Characterizations and Algorithms for Hyperequivalence, by Björn Victor, technical report DoCS 98/96.
Solos in Concert, by Cosimo Laneve and Björn Victor, ICALP'99 / MSCS 13(5) 2003.
Solo Diagrams, by Cosimo Laneve, Joachim Parrow and Björn Victor, TACS2001.

and Lucian Wischik's excellent overview of fusion research.

Björn Victor

Last modified: Sun, 06-Jul-2003 20:21 MEST