Applications
MERIT has potential applications in a wide range of mathematical optimization problems. We note that the case-dependent sub-optimality guarantees can be viewed as trust certificates provided along with the approximate solutions, and hence, are of practical importance in decision making scenarios.
To provide an example of MERIT's derivation, in the following, we consider unimodular quadratic programming (UQP), also known as complex quadratic programming. Interestingly, using MERIT one may obtain better performance guarantees for UQP compared to the analytical worst-case guarantees (such as 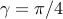 associated with SDR).
associated with SDR).
Unimodular Quadratic Programming (UQP)
The NP-hard problem of optimizing a quadratic form over the unimodular vector set arises in a variety of active sensing and communication applications, such as receiver signal-to-noise ratio (SNR) optimization, synthesizing cross ambiguity functions, steering vector estimation, and maximum likelihood (ML) detection. Namely, we study the problem
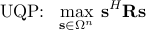
where 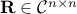 is a given Hermitian matrix, and
is a given Hermitian matrix, and  represents the unit circle, i.e.
represents the unit circle, i.e.
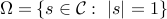 .
.
MERIT for UQP
To help the formulation of MERIT, Theorem 1 presents a bijection among the set of matrices leading to the same solution.
Theorem 1.
Let 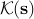 represent the set of matrices
represent the set of matrices  for which a given
for which a given 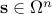 is the global optimizer of UQP. Then
is the global optimizer of UQP. Then
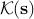 is a convex cone.
is a convex cone.For any two vectors
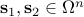 , the one-to-one mapping
, the one-to-one mapping
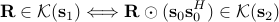
(where 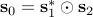 ) holds among the matrices in
) holds among the matrices in 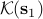 and
and 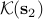 .
.
It is interesting to note that in light of the above result, the characterization of the cone 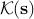 for any given
for any given 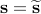 leads to a complete characterization of all
leads to a complete characterization of all 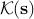 ,
, 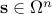 , and thus solving any UQP.
While a complete tractable characterization of
, and thus solving any UQP.
While a complete tractable characterization of 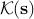 cannot be expected (due to the NP-hardness of UQP), approximate characterizations of
cannot be expected (due to the NP-hardness of UQP), approximate characterizations of 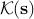 are possible. In the following, our goal is to provide an approximate characterization of the cone
are possible. In the following, our goal is to provide an approximate characterization of the cone 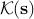 which can be used to tackle the UQP problem.
which can be used to tackle the UQP problem.
Theorem 2.
For any given 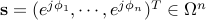 , let
, let 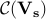 represent the convex cone of matrices
represent the convex cone of matrices 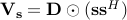 where
where 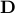 is any real-valued symmetric matrix with non-negative off-diagonal entries. Also let
is any real-valued symmetric matrix with non-negative off-diagonal entries. Also let 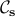 represent the convex cone of matrices with
represent the convex cone of matrices with 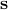 being their dominant eigenvector (i.e the eigenvector corresponding to the maximal eigenvalue). Then for any
being their dominant eigenvector (i.e the eigenvector corresponding to the maximal eigenvalue). Then for any 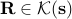 , there exists
, there exists 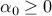 such that for all
such that for all 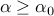 ,
,
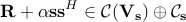
where 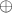 stands for the Minkowski sum of the two sets.
stands for the Minkowski sum of the two sets.
An intuitive illustration of the result in Theorem 2 is shown in Fig. 1. Indeed, it can be shown that Theorem 2 is valid even when 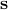 is a local optimum of the UQP associated with
is a local optimum of the UQP associated with 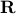 .
.
 |
Fig. 1. An illustration of the result in Theorem 2. |
Finally, one can use 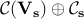 as an approximate characterization of
as an approximate characterization of 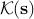 noting that the accuracy of such a characterization can be measured by the minimal value of
noting that the accuracy of such a characterization can be measured by the minimal value of 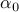 . Hereafter, we study a computational method to obtain an
. Hereafter, we study a computational method to obtain an 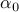 which is as small as possible. We also formulate the sub-optimality guarantee for a solution of UQP based on the above
which is as small as possible. We also formulate the sub-optimality guarantee for a solution of UQP based on the above 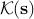 approximation.
approximation.
Using the previous results, we build a sequence of matrices (for which the UQP global optima are known) whose distance from the given matrix 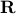 is decreasing. The proposed iterative approach can be used to solve for the global optimum of UQP or at least to obtain a local optimum (with an upper bound on the sub-optimality of the solution). We know from Theorem 2 that if
is decreasing. The proposed iterative approach can be used to solve for the global optimum of UQP or at least to obtain a local optimum (with an upper bound on the sub-optimality of the solution). We know from Theorem 2 that if 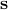 is a stable point of the UQP associated with
is a stable point of the UQP associated with 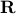 then there exist matrices
then there exist matrices 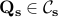 ,
, 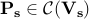 and a scalar
and a scalar 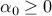 such that
such that 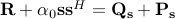 . The latter equation can be rewritten as
. The latter equation can be rewritten as
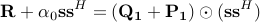
where 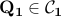 , and
, and 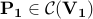 .
.
We first consider the case of 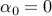 which corresponds to the global optimality of
which corresponds to the global optimality of 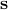 . Consider the optimization problem:
. Consider the optimization problem:
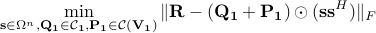
Note that, as 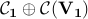 is a convex cone, the global optimizers
is a convex cone, the global optimizers 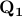 and
and 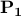 for any given
for any given 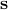 can be easily found. On the other hand, the problem of finding an optimal
can be easily found. On the other hand, the problem of finding an optimal 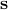 for fixed
for fixed 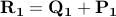 is non-convex and hence more difficult to solve globally.
is non-convex and hence more difficult to solve globally.
Note that there exist examples for which the above objective function does not converge to zero. As a result, the proposed method cannot obtain a global optimum of UQP in such cases. However, it is still possible to obtain a local optimum of UQP for some 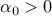 . To do so, we solve the optimization problem,
. To do so, we solve the optimization problem,
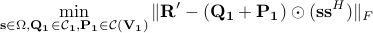
with 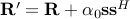 , for increasing
, for increasing 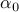 .
.
Sub-Optimality Analysis
We show how MERIT can provide real-time sub-optimality guarantees and bounds during its iterations. Let 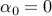 (as a result
(as a result 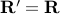 ) and define
) and define
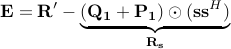
where 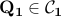 and
and 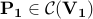 .
By construction, the global optimum of the UQP associated with
.
By construction, the global optimum of the UQP associated with 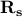 is
is 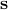 . We have that
. We have that
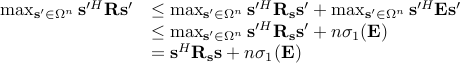
Furthermore,
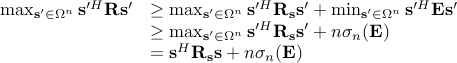
As a result, an upper bound and a lower bound on the objective function for the global optimum of UQP can be obtained at each iteration. Next, suppose that we have to increase 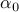 in order to obtain the convergence of
in order to obtain the convergence of 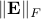 to zero. In such a case, we have that
to zero. In such a case, we have that
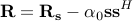
and as a result,

or equivalently,

The provided case-dependent sub-optimality guarantee is thus given by
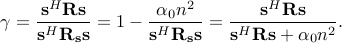
Numerical Examples and Discussion
We use the power method-like iterations, and MERIT, as well as the curvilinear search of with Barzilai-Borwein (BB) step size, to solve an UQP (with 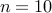 ) based on the same initialization. The resultant UQP objectives along with required times (in sec) versus iteration number are plotted in Fig. 2.
) based on the same initialization. The resultant UQP objectives along with required times (in sec) versus iteration number are plotted in Fig. 2.
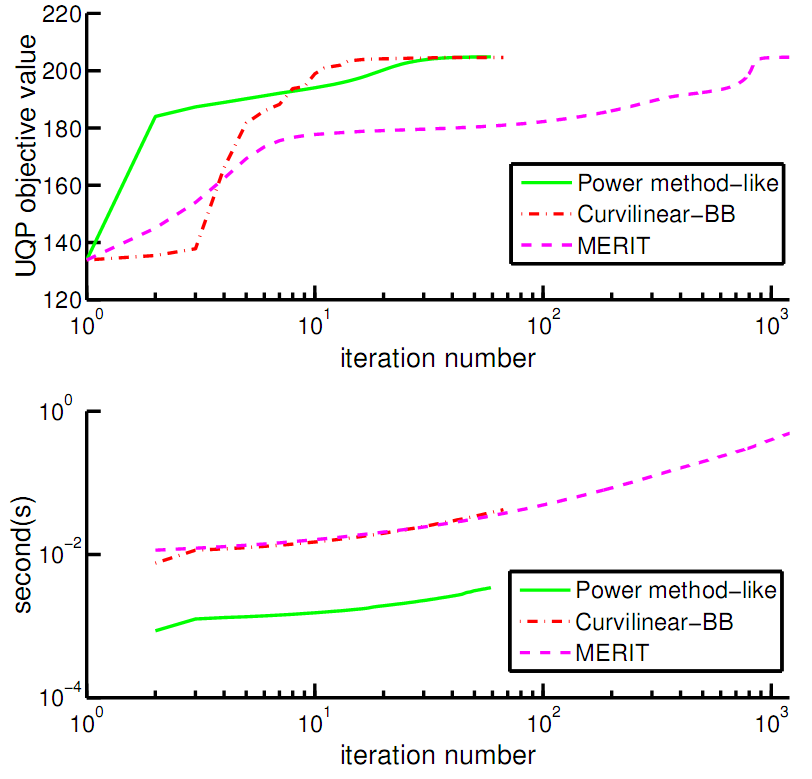 |
Fig. 2. A comparison of power method-like iterations, the curvilinear search with Barzilai-Borwein (BB) step size, and MERIT: (top) the UQP objective; (bottom) the required time for solving an UQP ( |
It can be observed that the power method-like iterations approximate the UQP solution much faster than the employed curvilinear search. On the other hand, both methods are much faster than MERIT. This type of behavior, which is not unexpected, is due to the fact that MERIT is not designed solely for local optimization; indeed, MERIT relies on a considerable over-parametrization in its formulation which is the cost paid for easily derivable sub-optimality guarantees. In general, one may employ the power method-like iterations to obtain a fast approximation of the UQP solution (e.g. by using several initializations), whereas for obtaining sub-optimality guarantees one can resort to MERIT.
Next, we approximate the UQP solutions for 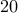 full-rank random positive definite matrices of sizes
full-rank random positive definite matrices of sizes 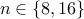 . Inspired by some previous works, we also consider rank-deficient matrices
. Inspired by some previous works, we also consider rank-deficient matrices  with rank
with rank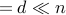 . The performance of MERIT for different values of
. The performance of MERIT for different values of 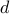 is shown in Table 1.
Note that, in general, the provided sub-optimality guarantees
is shown in Table 1.
Note that, in general, the provided sub-optimality guarantees 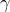 are considerably larger than
are considerably larger than 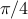 of SDR. We also employ SDR to solve the same UQPs. In this example, we continue the randomization procedure of SDR until reaching the same UQP objective as for MERIT. A comparison of the computation times of SDR and MERIT can also be found in Table 1.
of SDR. We also employ SDR to solve the same UQPs. In this example, we continue the randomization procedure of SDR until reaching the same UQP objective as for MERIT. A comparison of the computation times of SDR and MERIT can also be found in Table 1.

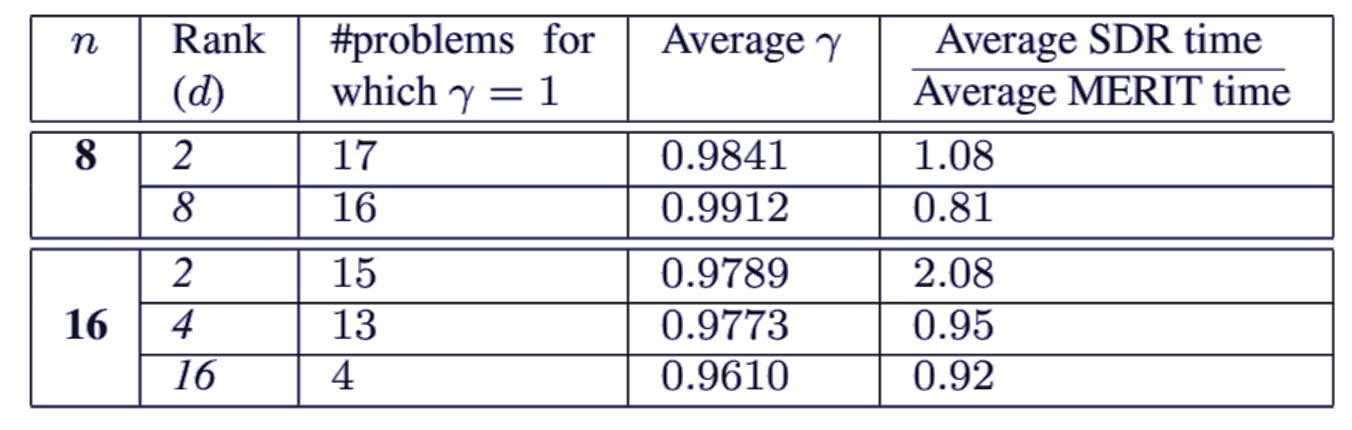 |
Table 1. Comparison of the performance of MERIT and SDR when solving the UQP for |

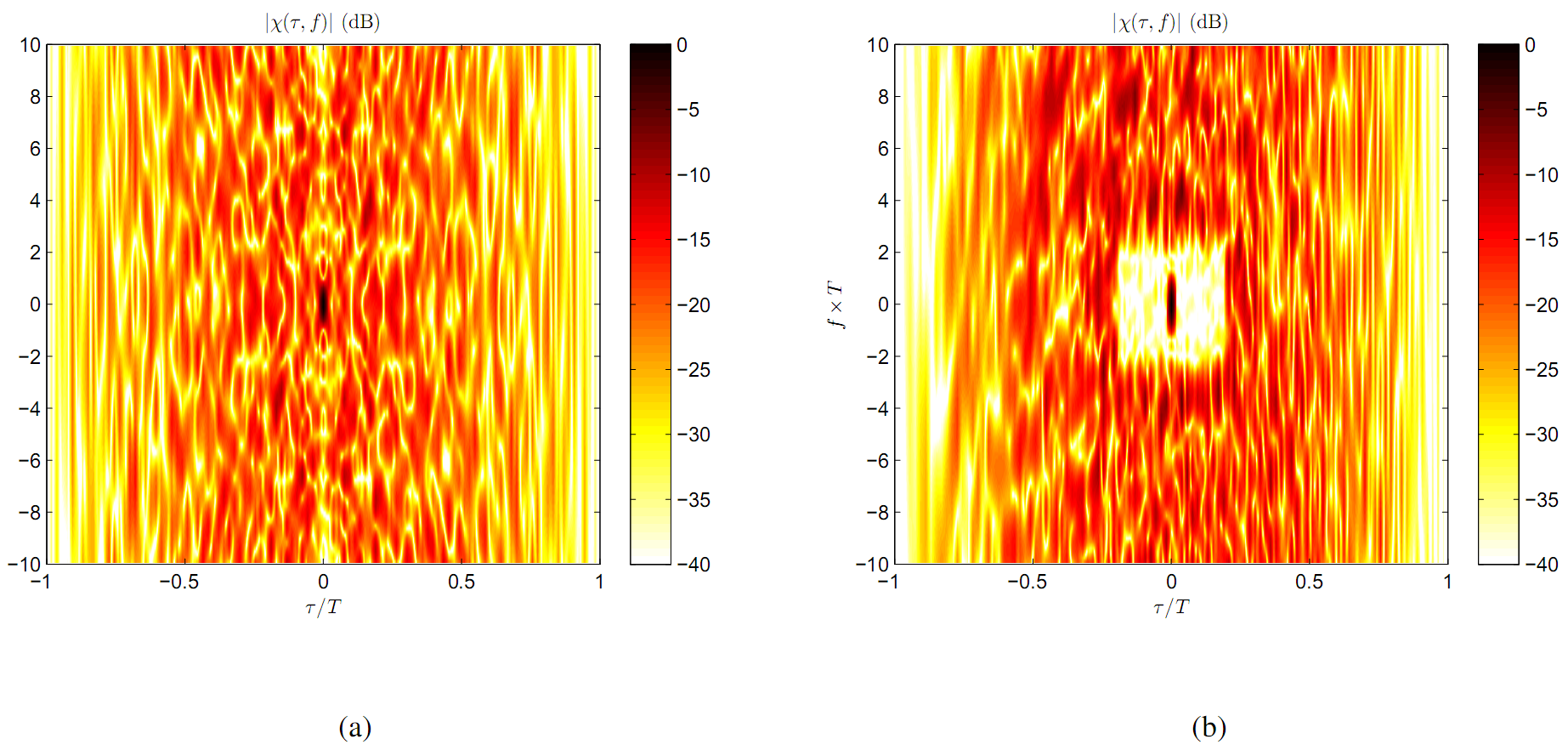 |
Fig. 3. Application of MERIT for designing cross ambiguity functions (CAFs). The normalized CAF modulus for (a) the Bj"orck code of length 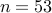 (i.e. the initial CAF), and (b) the CAF obtained by MERIT. See the Related Publications for more details.
(i.e. the initial CAF), and (b) the CAF obtained by MERIT. See the Related Publications for more details.
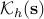 denotes the convex cone of matrices with
denotes the convex cone of matrices with 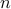 and ranks
and ranks