This page will detail the work presented in Approximations for Model Construction. The goal is to solve quantifier-free first-order constraints over theory of FPA. The procedure presented in the paper is an iterative approximation refinement procedure. The approximations used for FPA cannot be classified as either over- or under-approximations. The approximation changes the floating-point sort of the individual occurrences of operations and constants and changes them accordingly. Initially, all sorts are as small as possible and will (unless the model is obtained sooner) increase until they reach the sorts of the original problem. The procedure is built upon the bit-vector encoding of FPA and it's subsequent bit-blasting to a propositional formula.
About (the Theory of) Floating-Point Arithmetic
The Floating-Point Arithmetic is defined by the Standard IEEE 754-2008 (orig. 1985). The Theory of Floating-Point Arithmetic refers to the SMT-LIB theory which can be found here.Implementation
The described approach is implemented as a tactic within the Z3 SMT solver and the source code can be found here.Benchmarks
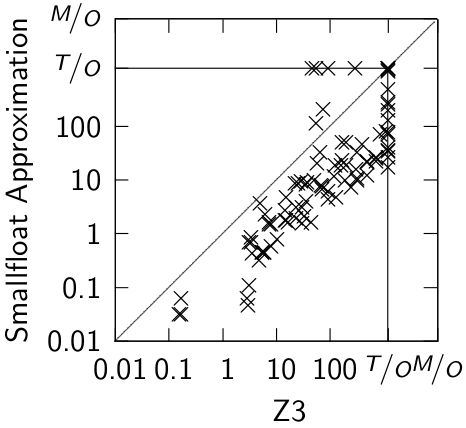
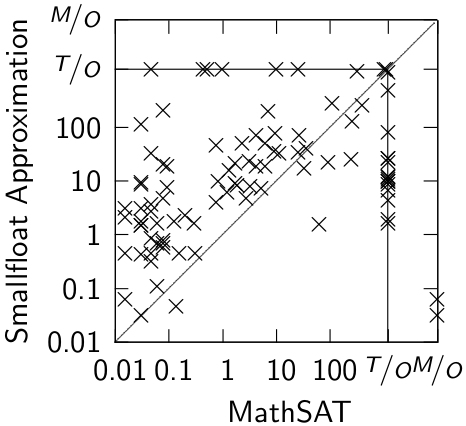
Benchamarks used in the paper have been used to evaluate the ACDCL approach to solving FPA found in MathSAT. The benchmarks originate from verification problems of C programs performing numerical computations, where ranges and error bounds of variables and expressions are verified; other benchmarks are randomly generated systems of inequalities over bounded floating-point variables.Experimental evaluation
We performed comparison with the base method (implemented in Z3) and the ACDCL approach (MathSAT).