We develop methodology and concrete tools for learning, reasoning and acting based on measured data. Two key aspects of our research are also the analysis and practical application of these methods. One of our cornerstones is a probabilistic model allowing us to systematically represent and cope with the uncertainty that is inherent in most data. A model is a compact representation (set of assumptions) of the data that in precise mathematical form captures the key features of the underlying system. An important goal is to develop flexible models that can capture complex dynamical phenomena and their environments allowing machines and humans to better understand the surrounding world.
The data and the model are two of the cornerstones of our research. The third cornerstone is the inference methodology. Inference relates to the fundamental objective of automatically constructing models based on data. Over the past decades we have experienced a continuous development of increasingly more powerful computational inference methods. However, for many highly relevant applications the state-of-the-art algorithms still struggle. For example, it remains a major challenge to develop efficient and accurate inference algorithms capable of handling high-dimensional models, data rich applications, complex model structures, and diverse data sources that arise in many of the data analysis problems that we are currently facing.
The fourth and final cornerstone of our research is that of control. The main task here is to make use of all that has been learnt from the data and represented within the probabilistic model to automatically make decisions and influence the current situation in a suitable manner. Most existing control approaches cannot explicitly account for and make use of uncertainty. We want to change this by using probabilistic models to develop new control strategies, that are better suited to operate in uncertain environments. From a methodological point of view we are open to most concepts. Our specialities include sequential Monte Carlo (particle filters) methods, Markov chain Monte Carlo, Gaussian processes, and deep (reinforcement) learning.
Collaborations with companies: ABB Crane Systems, Autoliv, Greenely, Saab, Sectra, and Xsens Technologies.
Collaborations within academia: here.
For a slightly more detailed overview of our research, see the more detailed selected topic descriptions below and/or the talks available here.
Model (parameter) learning
Find a probabilistic model (includes finding the static parameters) capable of explaining the measured data. We employ both Bayesian and maximum likelihood approaches.
Learning static parameters in nonlinear dynamical models
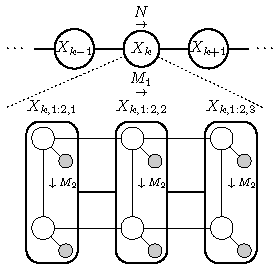
We work a lot on developing and using Sequential Monte Carlo (SMC) methods (i.e., particle filters and particle smoothers) for static parameter learning in nonlinear dynamical models. It is well known that SMC methods alone are not capable of solving the model learning problem. However, coupled with other algorithms, powerful inference tools can be devised. We have devised maximum likelihood solutions by combining the Expectation Maximization (EM) algorithm with SMC methods. We also work on Bayesian algorithms, mainly by developing and exploiting the Particle Markov Chain Monte Carlo (PMCMC) family of algorithms. This allows us to compute the posterior parameter distribution for general nonlinear dynamical models.
Representative publications: [C65], [J16], [J9], [J15], [J14], [C59].
Bayesian non-parametric (BNP) models
Flexible models are essential in explaining the complex world around us. Here, flexibility means the ability to adapt and to express uncertainty, not only over parameters, but also over structural aspects of the model, such as the number of parameters, segmentations and couplings. Bayesian non-parametrics offers flexible models of this type and when combined with suitable inference algorithms (that are starting to emerge) this constitutes a very promising technology. Indeed our new PMCMC algorithms have prooven very useful in solving the resulting learning and inference problems. Especially the particle Gibbs with ancesor sampling [C59] seems to be fit these problems nicely. The most commonly used BNP models are the Gaussian process (GP), the Dirichlet process and the Beta process. As an example, we have been able to construct and learn a GP state space model that for the first time allows for the entire nonparametric richness to be maintained [C65].
Representative publications: [C65], [C59], [J15], [J16], [C62].
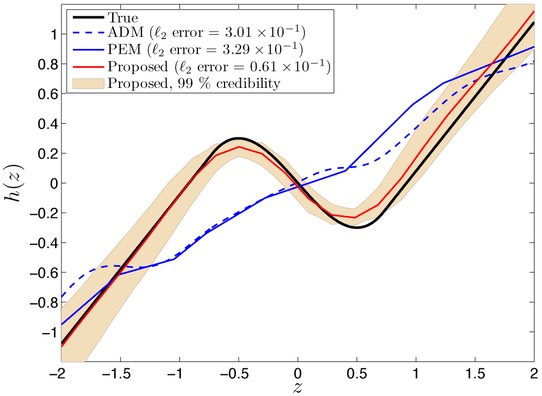
Learning Wiener models
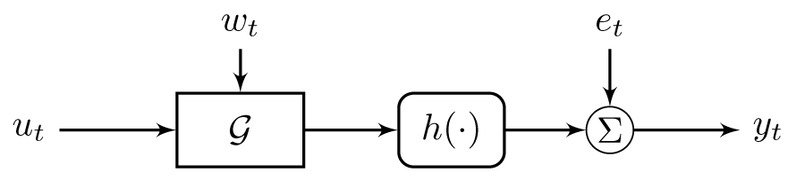
A Wiener model is a linear dynamical model followed by a static nonlinearity, which is illustrated in the figure. It offers a simple, but still very interesting step into the world of nonlinear dynamical systems. The solutions we provide can straightforwardly deal with (still of course requiring the model to be identifiable) noninvertible nonlinearities, multidimensional data, colored stochastic disturbances both before and after the static nonlinearity. We have derived both Maximum Likelihood and Bayesian solutions. The methods we are developing straightforwardly allows for the blind Wiener problem to be solved as a special case.
Representative publications: [J15], [J14], [C56], [C50].
State inference
Infer the state based on the information provided in the measurements. More concrete, this is about finding the conditional distribution of the state given the measurements.
Particle methods - algorithms and analysis
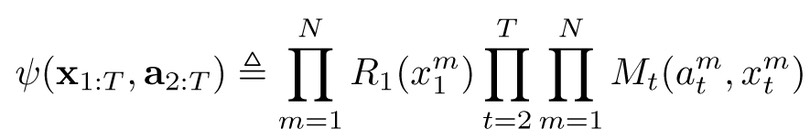
The Sequential Monte Carlo (SMC) family provides powerful solutions to the state inference problem in nonlinear dynamical models. The key idea is to maintain an empirical representation of the distribution of interest using a collection of weighted samples. Intuitively, each sample (a.k.a. particle) represents one hypothesis of the state of the dynamical system. The SMC methods provide provably correct algorithms for propagating these particles over time by exploiting the information present in the measurements. The most popular member of the SMC family is the so-called particle filter. We are also working developing particle smoothers (PS) capable of solving the state smoothing problem.
Representative publications: [J16], [J6], [C59], [J10], [C51], [J11].
Particle methods - exploiting model structure
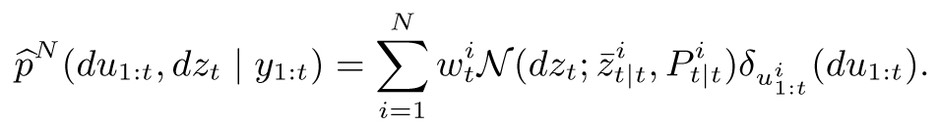
If there is any structure available in the model and/or the data this should be exploited in deriving a suitable inference algorithm. We have developed several algorithms of this type, especially for conditionally linear Gaussian state-space (CLGSS) models. For the filtering problem this results in a combination of the particle filter and the Kalman filter referred to as the Rao-Blackwellized particle filter (RBPF). For the smoothing problem we have recently developed an RBPS, which is an algorithm of the forward filtering/backward simulation type. The algorithmic components are a PF, a backward simulator PS and a linear smoothers (e.g., modified Bryson-Frazier or Rauch-Tung-Striebel). By exploiting the tractable substructure present in the CLGSS models, the RBPF results in more accurate estimators than a standard PF and it can therefore be used for filtering in even more challenging, e.g. high-dimensional, models.
Representative publications: [J1], [C64], [C49], [J2], [J7], [C6].
Exploiting map information within inference problems
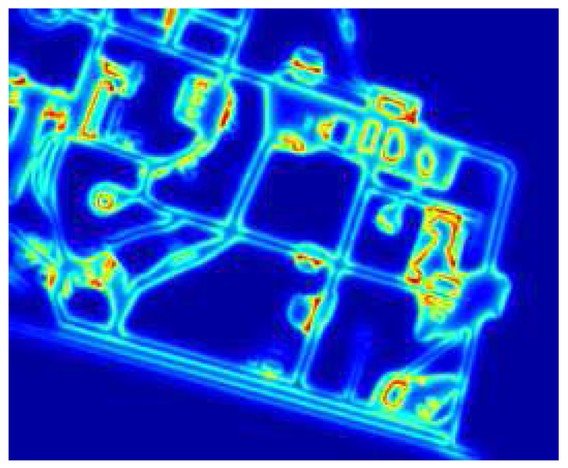
World models in the form of different type of maps are becoming more and more common. In solving for example localization and tracking problems, the information contained in these maps is highly valuable. One important reason for this is that they offer absolut information. We are developing inference algorithms capable of exploiting the information in these world models. This typically results in algorithms based on various particle methods, since they naturally allow for incorporation of map information. Besides exploiting previously existing maps we are also interested in the related problem of Simultaneous Localization And Mapping (SLAM), where the map needs to be inferred as well. When it comes to applications we have been working with for example active safety systems for cars, unmanned areal vehicles (UAVs) and target tracking.
Representative publications: [BC2], [J7], [C36], [C26], [C45], [C4].
Magnetic mapping and positioning
In this work we aim to simultaneously build maps (i.e., models) of the local magnetic field and at the same time position ourself using this map. The measurements stems from magnetometers and additional sensor data (such as for example accelerometers and gyroscopes). Magnetometers are now cheap and they are becoming more and more widely available. The map is built and represented using Bayesian nonparametric (BNP) models. The figure shows a visualization of a first Gaussian process model (obeying Maxwell's equations) that we have built to model the local magnetic field produced by an upside down table.
Representative publications: [C62], [C63].
Modeling, calibration and fusion of inertial sensors and cameras

The aim of this work is to provide the capability of performing sensor fusion using measurements from inertial sensors (accelerometers and gyroscopes) and a camera. Besides providing a dynamical model we also provide a new algorithm capable of solving the calibration problem, i,e., estimating the relative translation and orientation between the inertial sensors and the camera. This algorithm does not require any additional hardware, except a piece of paper with a checkerboard pattern on it. In pursuing this work an integrated sensor unit (shown in the figure).
Representative publications: [J8], [J5], [C24], [C22].
Modeling, calibration and fusion of inertial sensors and magnetometers/ultra-wideband

This work aims to provide new technology enabling real-time position and orientation estimation using measurements from inertial sensors and ultra-wideband (UWB) or inertial sensors and magnetometers. The custom build sensor unit is shown in the figure to the right. As part of this work we have also developed a novel calibration method to determine the clock parameters of the UWB receivers as well as their 3D positions. It exclusively uses time-of-arrival measurements, thereby removing the need for the typically labor-intensive and time-consuming process of surveying the receiver positions. Experiments show that the method is capable of accurately calibrating an UWB setup within minutes. Together with our sensor fusion procedure this provides a powerful system for indoor positioning. This technology has been leveraged into the product MVN MotionGrid by our industrial partner Xsens.
Representative publications: [C33], [C39], [C58].
Automotive applications - road geometry and vehicle motion estimation

We provide a sensor fusion solution for the problem of joint ego-motion and road geometry estimation by making systematic use of measurements from a forward looking radar and camera (infrared or standard), steering wheel angle sensor, wheel speed sensors and inertial sensors. The solution relies on dynamical models for the ego vehicle, the road and the leading vehicles. The proposed solutions have been tested and compared to existing algorithms, using measurements from authentic traffic environments on public roads in Sweden.
Representative publications: [J12], [BC3], [C46], [C32], [C29], [C28].
Acknowledgements
My research is funded by The Swedish Research Council (VR), The Swedish Foundation for Strategic Research (SSF) and Vinnova.