P = NP?
Två snarlika problem
Antag att vi har en sammanhängande graf, med noder och kanter.
Problem 1
Finns det en rundväg där varje kant ingår precis en gång?
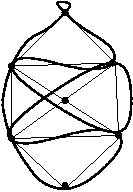
Svaret är "ja" om varje nod har ett jämt antal kanter.
En algoritm kan ge rätt svar i Ordo(antal kanter).
(Problemet formulerades av Euler, och är känd som
Königsberger Brücke problemet. Kanterna var broar mellan de öar
(noder) som Königsberg (numera Kaliningrad) ligger på.
Problem 2
Finns det en rundväg där varje nod ingår precis en gång?
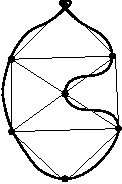
Problemet (Hamiltonian cycle problem) är svårt. Det är inte känd om
det finns en algoritm som löser det inom polinomiell tid.
P = NP?
P = mängden av problem som kan lösas inom polinomiell
tid av en algoritm.
NP = mängden av problem som kan lösas inom polinomiell
tid av en algoritm som får gissa (N = non-deterministic). Algoritmen
behöver bara lösa problemet om den gissar rätt.
Dvs
NP = mängden av problem där vi inom polinomiell tid kan avgöra om en
(gissad) lösningsförslag är en lösning.
Definitionen innebär att P är en delmängd av NP. Men datalogins
största fråga är: P = NP?
NP-svåra problem
Dessa är de svåraste problem inom NP. Dvs om det finns en
polinomiell algoritm får något problem i denna klass, då gäller P = NP.
Klassen är intressant, eftersom den innehåller många vardagliga
problem. Några exempel följer.
Hamiltonian cycle
Se ovan.
Travelling salesman
En handelsresande ska besöka ett antal städer i valfri ordning.
Vi har en avståndtabell mellan städerna. Vad är den kortaste
resrutten? (Eller, om vi vill ha en ja/nej fråga: finns det en resa
kortare än x?)
Bin packing
Vi har ett antal paket och ett antal behållare. Hur kan vi
lasta alla paket och använda så få behållare som möjligt
(eller: räcker n behållare)? Frågan kan tolkas i 3D (volym),
men även i 2D eller 1D (tex vikt, se boken) är problemet
NP-svårt.
Scheduling
Vi har ett antal uppgifter som tar tid. Vissa uppgifter är beroende
av andra. Vi har ett begränsad antal personer som kan utföra
uppgifterna. Vad är den kortaste tid vi behöver för att utföra alla
uppgifter (eller: går det inom tid t).
Problemet kan också formuleras i termer av studenter, lokaler,
och undervisningstimmar.
Logisk sanning
Given en logisk formell, är formelln alltid sant?
Ett bioinformatikproblem
Se Forskning och Framsteg 4/01. En kort sammanfattning finns
här, men den tar inte upp
problemet. En kopia av hela artikeln finns i STS-biblioteket.
Reduktion
Hur kan man bevisa att ett problem är NP-svårt?
Tekniken, reduktion, liknar den som vi har använt för att bevisa
att ett problem X är oavgörbart:
Bevis att "om vi kan lösa X i polinomiell tid, då kan vi
lösa ett känt NP-svårt problem i polinomiell tid."
Dvs, vi bygger en algoritm som lösar det kända problemet, och får
använda anrop till en funktion som lösar X-problem. Vi kan
förbehandla det kända problemet så att det blir ett X-problem, men
förbehandlingen får ta endast polinomiell tid (det är ju
X-lösaren som ska göra det svåra jobbet, inte förbehandlingen).
Lösningar
Människor kan inte heller snabbt hitta en optimal lösning. Däremot
är människor bra på att hitta nästan optimala lösningar.
I många fall räcker det att hitta en lösning som är "god nog".
Människor lyckas speciellt bra om problemet kan
visualiseras. Det är kanske svaret på boken, som undrar
"We might wonder why, if such a method (for solving NP-complete
problems) existed, evolution had not built it into our brains."
Även algoritmer kan försöka hitta lösningar som är bra, fast inte
optimal, inom polinomiell tid. Dessa algoritmer använder
heuristiker (tumregler), för att gissa sig fram till en bra
lösning. Detta är en (liten) del av området Artificiell
Intelligens.


