Mathematics and numerics in PDE-constrained optimization problems
with state and control constraints
Project highlights:
Optimal design, optimal control and parameter estimation of systems governed by
partial differential equations (PDE) give rise to a class of problems referred
to as PDE-constrained optimization (OPT-PDE).
OPT-PDE pursues the idea to influence phenomena and processes, governed by PDEs.
As PDEs describe almost every aspect of physics, chemistry, engineering, biology,
finance etc., that fit into a continuum framework, OPT-PDE can
be regarded as the ultimate/farthermost
goal of any application problem to steer the underlying systems in a desired way.
As a starting point, we consider the OPT-PDE setting with a stationary or time-dependent reaction-diffusion equation as constraint, combined with pointwise (box)
constraints of the state and the control variable, which latter is in addition sparse (localized).
The aim of the project is two-fold. On the modelling and discretization side we will
- study appropriate formulations of the cost functional and regularization techniques;
- by proper stabilization handle constraints and problem features applied on subregions of the control domain, not
aligned with any discretization mesh;
- analyse the interplay between regularization, stabilization and discretization parameters in
order to formalize their mutual dependence and how to balance the corresponding errors,
the ill-conditioning of the arising algebraic systems of equations and the attainable accuracy of the
computed optimal solution.
On the solution method side we will
- develop efficient preconditioners to speed up the
linear solvers, used in the nonlinear solution procedure, inevitably required for the target OPT-PDE
problem;
- develop two- and multilevel mixed nonlinear-linear methods to reduce the computational
cost of the nonlinear solver on the finest discretization level, required to guarantee a desired level
of accuracy;
- on all stages of development and implementation of the solution
procedures and algorithms, enhance their performance on HPC resources.
First results:
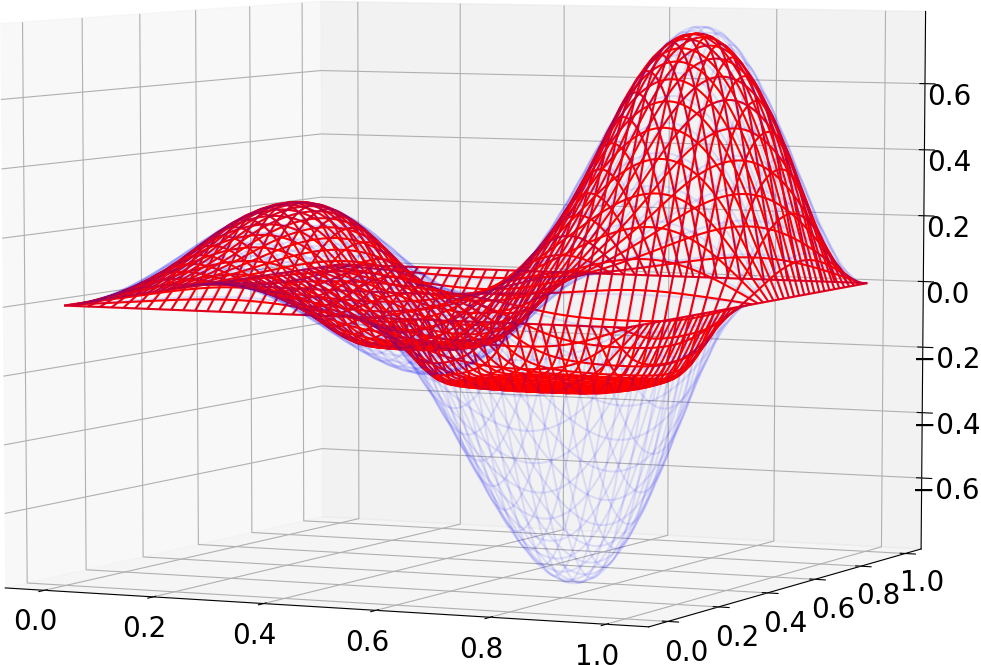 |
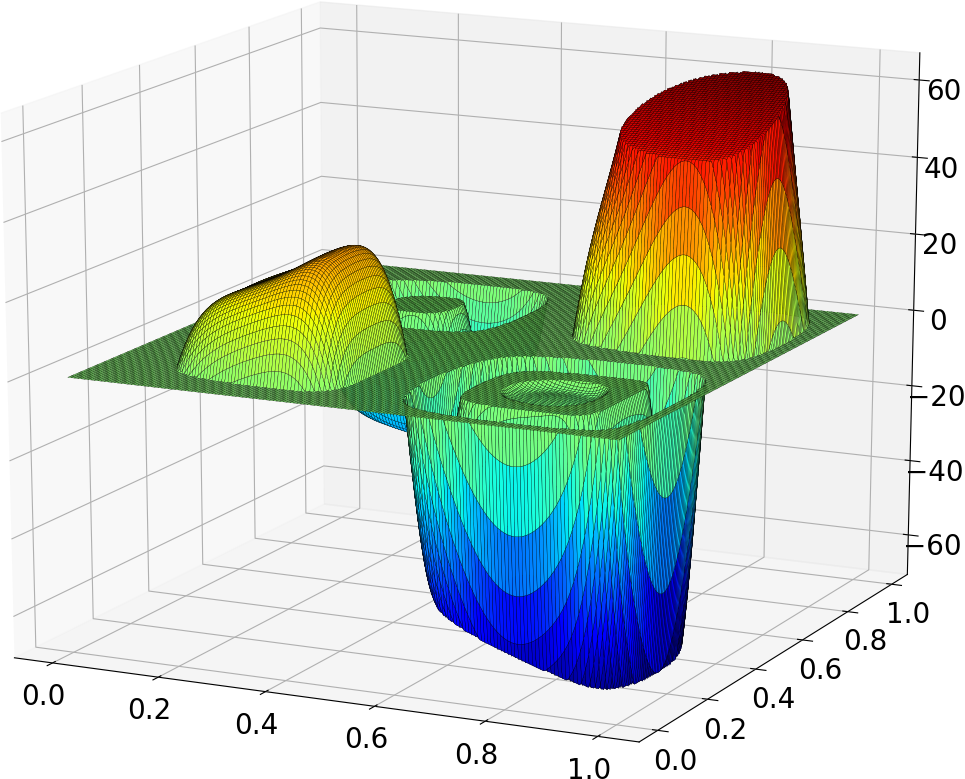 |
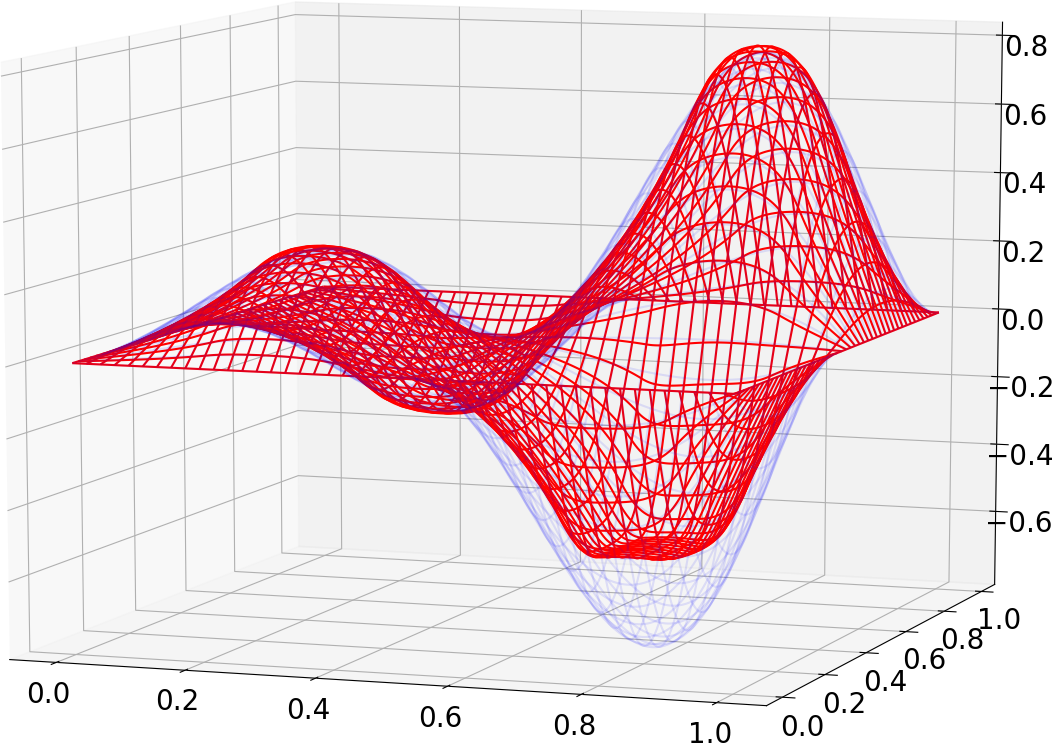 |
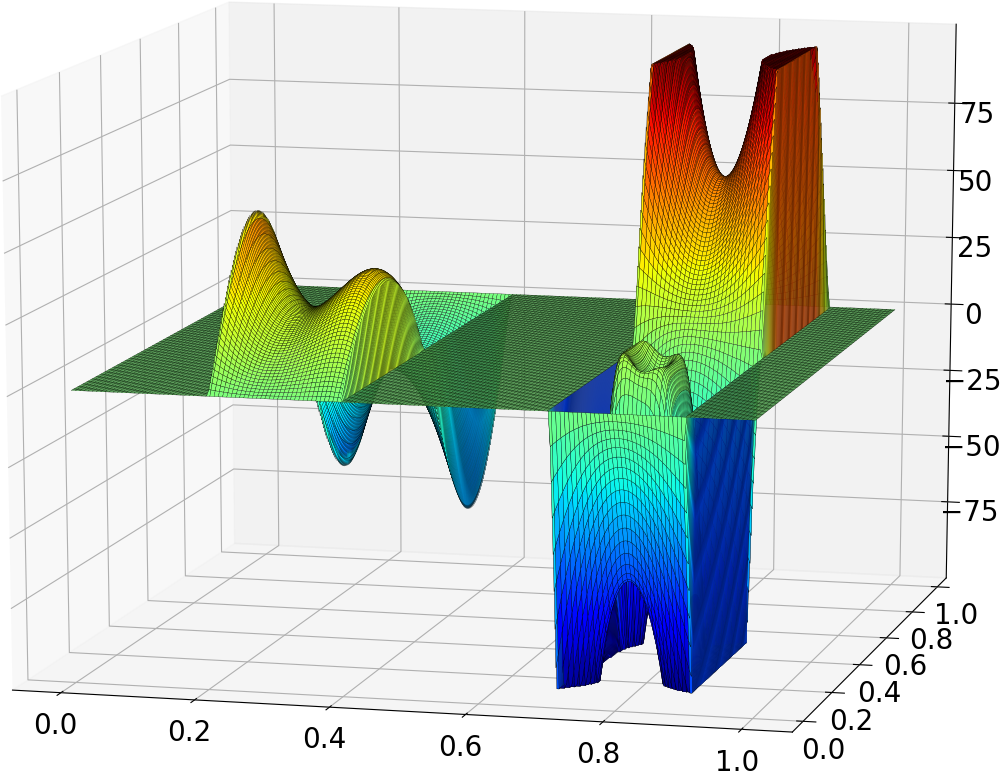 |
| State | Control | State | Sparse control |
Article in review: I. Dravins, M. Neytcheva,
PDE-Constrained Optimization: Matrix Structures and Preconditioners
As a far goal, the constraint could be extended to a system of equations, to model coupled heating-cooling physics processes.
| Maya Neytcheva Gunilla Kreiss Ivo Dravins |
| Scientific Computing, Uppsala University |
Last changed on March 11, 2017
Mail to: Maya dot
Neytcheva "at"
it dot
uu dot se "







