Participants:

Gunilla Kreiss (Scientific Computing, Uppsala University)

Maya Neytcheva (Scientific Computing, Uppsala University)

Summary:

This project aims at constructing highly efficient preconditioners for problems discretized using the Finite Element method, and in particular locally adapted discretizations.

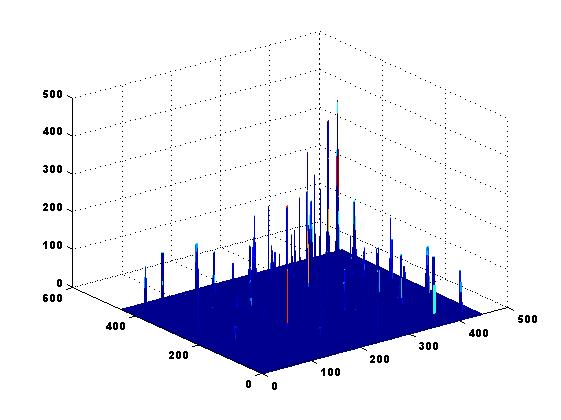
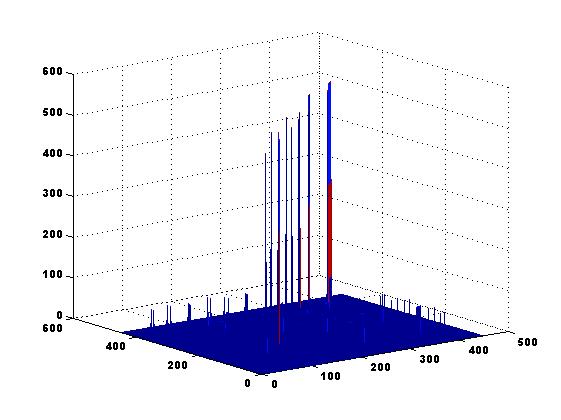
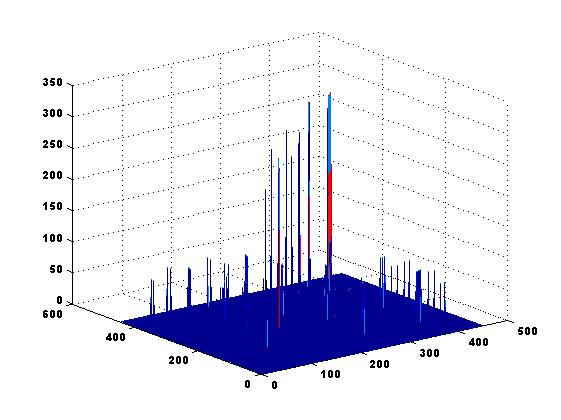
Recent work has shown that the Finite Element framework enables us to construct numerically efficient, sparse and computationally cheap approximations of matrix inverses. The method is based on local Finite Element aggregates and is thus easily parallelizable. The framework is suitable for different types of problems - symmetric, unsummetric, with discontinuous coefficients and of saddle point form. The so-constructed sparse approximate inverses are insensitive to coefficient jumps and discretization parameters. They capture quite well the structure of the exact inverse which has been problematic for other types of methods. The latter is illustrated on the figure below, for a problem with coefficient jumps of order 1000. One can observe that both the order of magnitude and the position of the largest entries of the matrix inverse are well captured by the constructed approximation.

Exact matrix inverse ....................... and ......................... Approximated matrix inverse

Approximated matrix inverse improved using Frobenius notm minimizing correction

We intend to extend the approach to a broader class of problems, namely problems with anisotropies, general unsymmetric problems, for instance as arising in time-dependent phenomena, modelled by coupled systems of Partial Differential Equations.

One of the target application problems for the project is the solidification of a pure material from its undercooling melt, taking into account various effects such as surface tension, kinetic undercooling and crystalline anisotropy.