Emilie Blanc - Post Doctoral

Uppsala University
Department of Information and Technology
Division of Scientific Computing
Lägerhyddsvägen 2
Box 337
SE-751 05 Uppsala
Sweden


Email :
ITC building  2, floor  4, room  2441
Phone : (+46) 1 84 71 27 66
Mobile : (+46) 7 22 51 92 52


CV
Thesis: wave propagation in porous media
Post Doctoral: reaction-diffusion in living cells
Publications
Congress
Seminars
Teaching

Photo

CV


Thesis

Title: "Time-domain numerical modeling of poroelastic waves: the Biot-JKD model with fractional derivatives"

Supervisors: Guillaume Chiavassa (M2P2, Marseille, ) and Bruno Lombard (LMA, Marseille, ).

I have investigated the propagation of poroelastic waves described by the Biot’s model in the time-domain. Most of the existing methods have been developed in the low-frequency range. The aim of my thesis was to derive some numerical methods in all the domain of validity of the Biot’s model. In the high-frequency range, the effects of the viscous boundary layer inside the pores must be taken into account. The model of dynamic permeability of Johnson-Koplik-Dashen (JKD) is used. In this case, some coefficients of the Biot-JKD’s model are proportional to the square root of the frequency. In the time-domain, fractional derivatives are therefore introduced into the evolution partial differential equations.

Two strategies exist to calculate these fractional derivatives. The first strategy is to compute the involved convolution integral. However, it requires to store the past of the solution, which is too penalizing in term of computational memory. The second strategy, which I implement, is based on a diffusive representation of the convolution kernel. The latter is replaced by a finite number of memory variables that satisfy local-in-time ordinary differential equations. The coefficients of the diffusive representation are determined by nonlinear optimization on the frequency range of interest.

The properties of the Biot-JKD’s model with diffusive representation are analysed: hyperbolicity, decay of energy, error of the model. A splitting strategy is then applied numerically: the propagative part of Biot-JKD equations is discretized using a fourth-order ADER scheme on a Cartesian grid, whereas the diffusive part is solved exactly. An immersed interface method is implemented to discretize the geometry on a Cartesian grid and also to discretize the jump conditions at interfaces. Numerical experiments are presented, for isotropic and transversely isotropic media. Comparisons with analytical solutions show the efficiency and the accuracy of this approach. Some numerical experiments are performed to investigate wave phenomena in complex media: influence of the porosity of a cancellous bone, multiple scattering across a set of random scatterers.


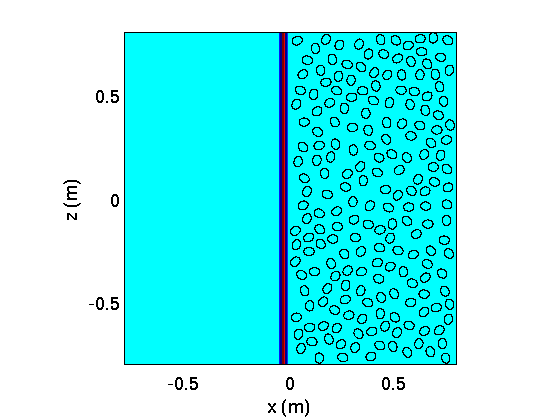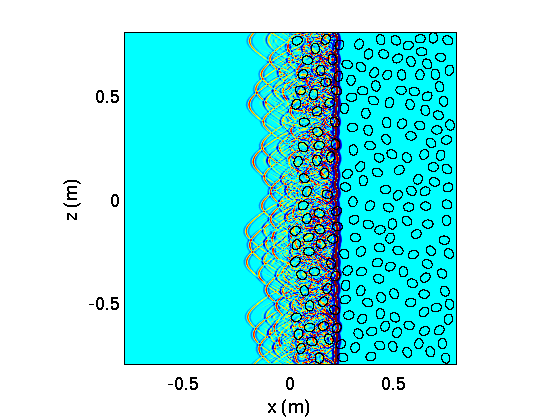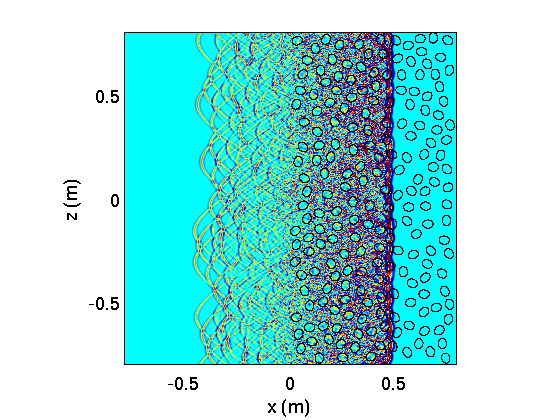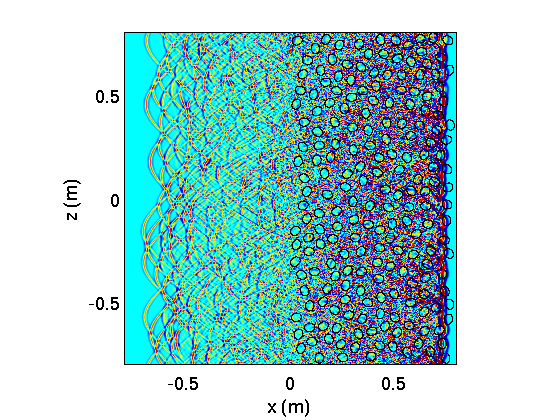
multiple_scattering.gif
Wave propagation across a porous medium including 200 ellipsoidal scatterers

Post Doctoral

Title: "Numerical modeling of reaction-diffusion system : subdiffusion and molecular crowding in living cells"

The signature of Brownian diffusion is the linear asymptotic dependence of the mean square displacement of the diffusing particle on time. The signature of anomalous diffusion is a non-linear dependence on time. Asymptotically, the mean square displacement is proportional to a non-integer power of the time. If the exponent is less than one, the particle is said subdiffusive. The subdiffusion of these molecules in living cells is then slower than Brownian diffusion. The subdiffusion in living cells might be advantageous. For instance, it leads to higher reaction efficiency. Biochemical reactions often involve initiation barriers. A reactant that diffuses normally could swiftly escape its target before it is had time to interact. In certain models, the chance of finding a nearby target is explicitly increased by subdiffusion.

At the mesoscopic Continuous Time Random Walk (CTRW) model, the waiting-time probability density function is proportional to a negative non-integer power of the time. From this model, one obtains at the macroscopic level a continuum evolution equations, with a fractional derivative in time.

Using a diffusive approximation on N points, the waiting-time probability density function of the CTRW model is approximated by a sum of decreasing exponentials. This new mesoscopic model is called multistate CTRW. From it, at the macroscopic level, we derive a system of reaction diffusion equations, where the N pseudo-species diffuse normally. The concentration profile of the species that shows subdiffusive behavior is given by the sum of the pseudo-species.

The system thus obtained is stable and conserves mass. It also has the desired property of showing return to normal diffusion for long time scales.

Publications


Congress


Seminars


Teaching