The assignment provides experience with developing and simulating TTPN models of concurrent systems. It is designed to reinforce the following areas of the curriculum.
Please see the Departmental handbook for full details on the procedures related to the administration and return of assignments.
Plagiarism is the process of claiming that work done by others has been done by you. Please note that the Department has a policy on plagiarism in assignments and you should consult the relevant Departmental handout for full details.
Submission will be electronically managed via the commands submit and verify. To submit your assignment create a directory called "PAR". Copy into that directory the following files.
Execute the command "submit PAR<CR>" to send the contents of the directory to the submission site. You can check that the submission has been successful by issuing a "verify" command. If you make an incorrect submission resubmit using the "submit" command again. This will overwrite your previous submission.
Transition timed petri-nets (TTPN's) are a significant part of the modelling section of the CSE31PAR course. They allow us to model systems that include the notion of delay between state transitions. We have formulated TTPN models for a range of situations and we have discussed the idea of simulating TTPN models in order to answer efficiency and safety questions for complex models. This technique can be used in conjunction with reachability analysis to answer a range of questions.
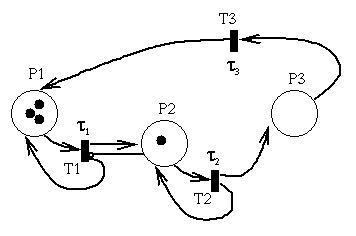
The simulations are to be conducted using the simulation package PN_Sim which is available from this assignment page. To carry out the simulation part of the assignment you will need to understand how the data structures in the file "timing.src" are set up to represent a TTPN. The file currently contains code which models the following TTPN. This example should help you understand what the data structures and timing delay functions do.

The firing delay for transitions is regulated by three delay functions.
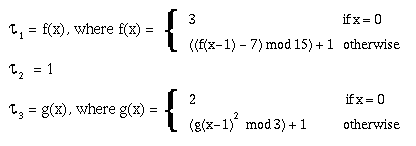
A commercial transportation company maintains a fleet of vehicles with which to transport items orderd by its customers There are two types of vehicle in service, cars and motorcycles.
Each type of vehicle can be in one of four states, "in use", "broken", "under repair", "idle". Studies show that the time to repair a car can be modelled by a function T_rc which is a random number of time units between 6 and 13. Similarly T_rm (for motorcycles) is a random value between 2 and 8 time units.
Customer requests arrive at a central dispatch location at a rate that can be modelled using an inter-arrival time delay set to the following function T_rq= exp(1/x), where x is a random value in the range (0.1,0.6]. These requests are distributed to cars or motorcycles in a ratio that is modelled as exactly 2:1.
In addition the following factors are needed to produce a complete system model.
Design, draw, label and explain the assumptions used to derive a TTPN model which describes this system.
Download the PN_Sim simulation package, using this link, and compile it on your UNIX account. To compile the simulation you need to un-tar the simulation files and type "make" in the PN_Sim directory.
Implement your model within the simulation by altering the data structures and functions defined in the file "timing.src".
To collect statistics about the system you will need to extend the data structures in the file "kernel.src" to include new data structures to keep track of the contents of the marking MU over the duration of the simulation. These structures should be updated in the function "Stats", which currently prints the contents of MU and the global virtual time (GVT) to the screen. Note that the current version of the Stats function also checks that a safety property of the sample net is not violated. You will need to remove this check when simulating your TTPN.
Using your model collect appropriate statistics with which to answer the following questions. Assume that each time unit refered to above is an hour. Simulate the system for a month (assuming 24 hour service) and answer the following questions.
This document was generated using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 Paper.tex.
The translation was initiated by Arnold N. Pears on Mon Dec 21 13:30:52 AEDT 1998