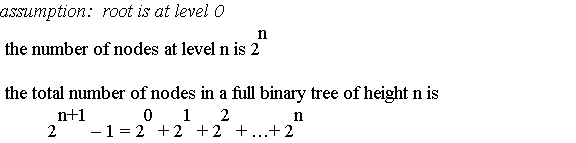Linear vs. non-linear
collections of objects
|
non-linear
|
|
access of elements is sequential
|
access along branching paths
|
|
unique first element
|
may be many "first" elements
|
|
unique last element
|
may be many "last" elements
|
|
each interior element has a unique successor
|
each element may have multiple successors
|
|
one-dimensional
|
two-dimensional (or more)
|
e.g.:
vectors
linked lists
stacks
queues
|
e.g.:
graphs
|
Trees
A note on graphs
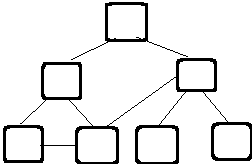
Tree terminology
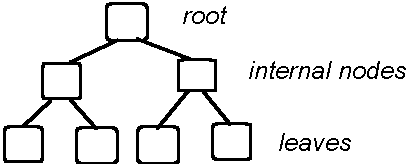
Tree genealogy
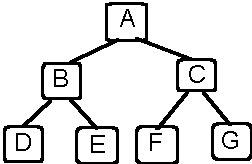
Subtrees
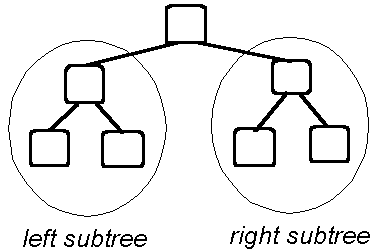
Degree of a tree
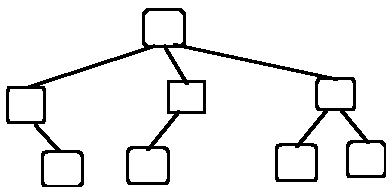
tree of degree 3
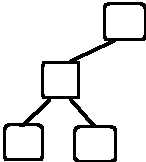
tree of degree 2
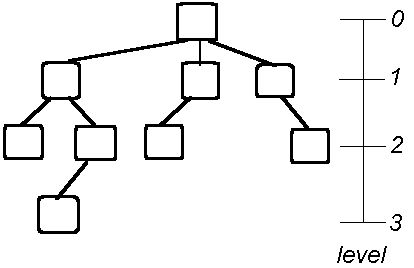
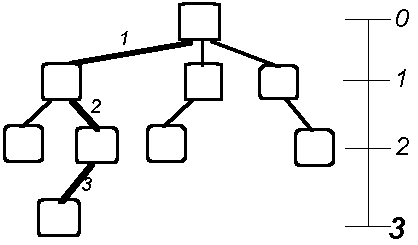
Level of a node
the level of a node is defined
by its path: it's a count of the number of arcs between the node
and the root
- - root level is zero
- - children of root are at level one
- - grandchildren of root are at level two
- - etc.
Depth or height of a tree
Density of a tree
- density is related
to the number of nodes per level of the tree
- measures the size of a tree by considering the
number of nodes in the tree relative to the depth of the tree
- the potential density of a tree is related to
its degree
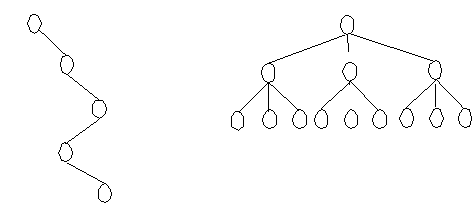
Two extremes of tree density
- degenerate tree
- - a "thin" tree
- - has only one leaf node
- - the root and each interior node has only one
child
- => to which data structure is this equivalent?
- full tree
- - every non-leaf node has maximum number of children
allowed by the degree of the tree
Advantages of higher density
- the path length from root to any node in the
tree is less for denser trees
- there are proportionately more elements near
the top of dense trees
- dense trees allow for
- - large collections of data
- - rapid access: time proportional to the height
of the tree
- Caution !!
definitions can vary slightly from author
to author:
- - some authors define the root as being at level
"1" rather than level "0"
- - some authors say that an empty tree has depth
"0" and that a one-node tree has depth "1"
Moral: State your assumptions!!
Examples of trees
- family tree
- company organization
- parse tree
- expression tree
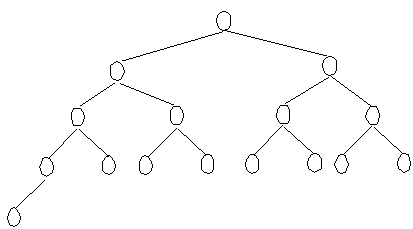
Binary trees
- recursive definition of a binary tree:
- - the empty tree is a binary tree
- - a node whose left child is a binary tree and
whose right child is a binary tree is a binary tree
- the subtree rooted at the left child of a node
is its left subtree
- the subtree rooted at the right child of a node
is its right subtree
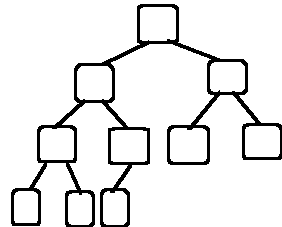
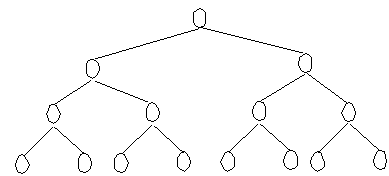
Complete binary trees
- the top n-1 levels form a full tree
- the leaf nodes at level n occupy the left-most
positions
i.e. the leaves are filled in from left to right
- the longest path from the root to a leaf is O(log
n)
=>maximal number of leaves with minimal path length
Properties of full binary trees
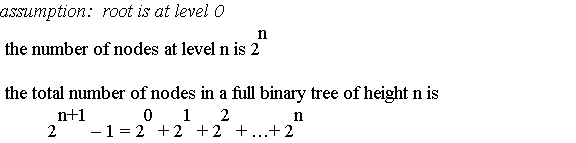
Properties of complete binary trees
- M, the number of nodes in a complete binary tree
of height n, satisfies the inequality

- solving the inequality for n gives
n < log M < n + 1
- this gives a formula for finding the minimum
depth of a binary tree
B>Properties of path length
- A binary tree with M nodes will have at least
one path with path length floor(log M)
- In a complete binary tree with M nodes:
- longest path has length floor(log M)
- - longest path traverses ceiling (log M) nodes
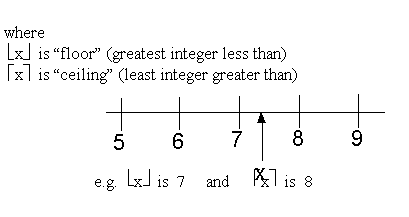
Consider a tree where M , the number of nodes in
the tree, is 10,000
- for a degenerate tree with M nodes, there's one
path:
-
- for a complete binary tree with M nodes:
- maximum path length
- = floor (log 10,000 )
- = floor(13.28)
- = 13
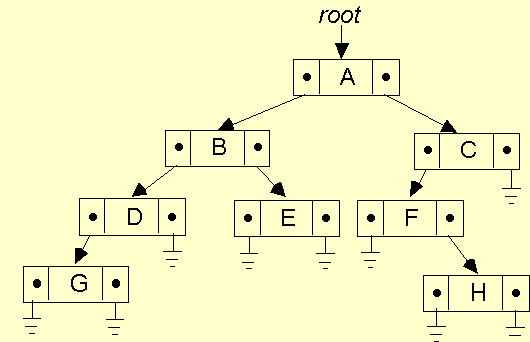
Implementing binary trees
- - a field for the data value
- a pointer reference to the root of the left subtree
- a pointer reference to the root of the right subtree
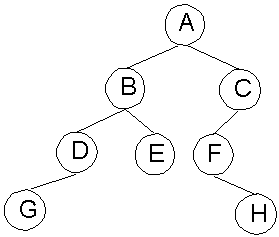
Example:
- correspondence between an abstract tree and its
tree implementation
Choices for implementation
- vector-based implementation
- - good representation if the tree is relatively
full
- - poor if tree changes frequently
- pointer-based implementation
- - good if tree changes frequently
- allows dynamic management of nodes
- - Budd's implementation, the node
class, is defined beginning on p. 285
Manipulating binary trees
Tree traversals
- want to visit every node in the given tree
- since non-linear, there are several possible
orders for the visit
- regardless of the order of visits, will want
to access
- - the root (or node)
- - the left subtree
- - the right subtree
- the order of visitation can vary
- - the node may be visited 1st, 2nd, 3rd
- - left subtree may be 1st, 2nd, 3rd
- - right subtree may be 1st, 2nd, 3rd
a total of six different organized orderings
NLR LNR LRN NRL RNL RLN
Traversal types