Lambdakalkylen ger också en beskrivning av begreppen beräkning och beräkningsordning.
Grundläggande i lambdakalkylen är tre regler för förenkling/beräkning, alfa, beta och eta-reglerna. Med vissa val av representationer, om alla objekt, även de naturliga talen, avbildas på funktioner, kan alla beräknningar utföras med dessa tre regler.
En denotationssemantik är i princip en funktion som tar ett argument, en programspråkskonstruktion, och returnerar en bild av konstruktionens betydelse.
Antag att vi hittar på ett nytt språk och beskriver dess betydelse med en denotatonssemantik. Om vi implementerar denna funktion (denotationssemantiken) i ett existerande programmeringsspråk (t ex Lisp), så har vi alltså en funktion som översätter från vårt nya språk till Lisp. Därmed har vi en interpretator för vårt nya språk och kan evaluera uttryck i detta.
Skriv en funktion som reducerar ett lambdauttryck så långt det går. Avbilda de naturliga talen på lambda-uttryck och räkna ut uttryck såsom 1+1=2 i denna representation.
Skriv och implementera en enkel denotationssemantik för ett funktionellt språk i Lisp.
Skriv och implementera en enkel denotationssemantik för ett funktionellt språk i Prolog.
Petersson, Beräknebarhet för dataloger, Aquila
Barklund, Kursmaterial för Program och Maskinsemantik, utdrag
Gamla föreläsningsanteckningar, vissa böcker i utdrag i kursbiblioteket
Lisp har inte lat evaluering, utan i stället ivrig evaluering. I Lisp utvärderas således alla uttryck (dvs alla funktionsparametrar) direkt, oavsett om resultatet behövs eller inte.
Ett exempel får klargöra. Antag nedanstående funktionsdefinitioner:
(defun fac(n)
(cond ((= n 0) 1)
(t (* n (fac (- n 1))))))
(defun funk (a b)
(cond ((= a 3) t)
(t b)))
Studera följande anrop i Lisp (med ivrig evaluering):
(funk 3 (fac -4))
Denna utvärdering stannar inte, eftersom 3 och (fac -4) , enligt Lisps utvärderingsregler, utvärderas innan parametervärdena överförs till funktionen funk , och det andra argumentet ju aldrig terminerar.
I en tänkt Lisp med lat evaluering, skulle aldrig den andra parametern någonsin utvärderas i detta exempel, eftersom värdet av den inte behövs för att beräkna resultatet. I en sådan Lisp skulle exempelanropet således returnera värdet 3.
Lat evaluering kan användas bl a för att bygga datoriserade modeller av förlopp, som i teorin kan ha hålla på en oändlig tid, eller returnera ett oändligt antal värden.
Exempelvis kan vi diskretiserat modellera en signalkälla utan att i modellen förutsätta att källan endast är verksam en viss tid. Vi kan också skapa en lista innehållande exempelvis alla naturliga tal.
Sådana strukturer implementeras naturligtvis inte genom att försöka lagra alla värden - det är ju naturligtvis omöjligt. I stället r det lämpligt att lagra strukturen i form av ett par, som består att ett uträknat värde samt en funktion, som när den anropas, räknar ut nästa värde samt en funktion, som när den anropas räknar ut det därpå följande värdet och en funktion som .....
I en tänkt Lisp med lat evaluering skulle följande funktionsdefinition och anrop vara meningsfyllt:
(defun alla-heltal (n)
(concat n (alla-heltal (+ n 1))))
(alla-heltal 1)
Funktionsanropet skulle naturligtvis inte returnera alla heltal, utan enbart det första, följt utav en en funktionsdefinition.
För att kunna skriva ut ett bestämt antal av första talen i den tänkta listan krävs en speciell funktion, som exempelvis skulle kunna anropas på detta sätt:
(skriv-ut 50 (alla-heltal 1))
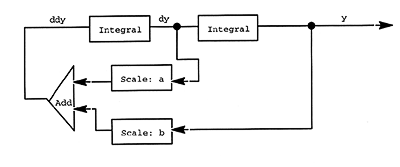
Ledning 1: Du kan upptäcka ett behov av att explicit anropa force och delay
Ledning 2: Nedanstående signalflödesdiagram kan säkert vara till hjälp.

b) Generalisera funktionen så att den kan approximera differentialekvationer av typen
d2y/dt2 = f(dy/dt, y)
Lös självständigt några uppgifter:
Uppgifter på höfar.
Studera avsnittet om lat evaluering och streams i Abelson-Sussman.
"översätt" några av funktionerna från Scheme till CommonLisp, testa.
Skriv självständigt ett par funktioner som returnerar en ström av alla heltal.
Skriv självständigt funktionen skriv ovan.
Studera avsnittet om streams och differentialekvationer i Abelson-Sussman.
Lös uppgiften.
Föreläsningsanteckningar från föregående års kurs.
Luger, Stubblefield Artificial Intelligence and the Design of Expert Systems, Benjamin Cummings. I ett appendix finns strömmar implementerade i Commonlisp.
Abelson-Sussman Structure and Interpretation of Computer Programs MIT Press. Här finns streams väl belyst med bra exempel, men i Lispdialekten Scheme.
Henderson Functional Programming Application and Implementation, Prentice-Hall. Kapitel 8 behandlar lat evaluering och oändliga strukturer, men är ibland svårsmält.
Andra CommonLisp-böcker i kursbiblioteket kan innehålla användbara exempel.
Ett par exempel kan illustrera den mycket kompakta programkoden. Om du läser denna "som matematik" och inte "som data", är den lättförståelig.
Exempel 1
[n * n | n <- [0 ..]] en lista av kvadraten av alla heltal från 0
Exempel 2
[r | r <- [1 .. n div 2]; n mod r = 0] en lista av faktoriseringen av n, ty
r är varje tal mellan 1 och n/2 och n
modulo r är noll
Exempel 3
quicksort[]=[]
quicksort(x:xs) = quicksort[y | y <- xs; y<x]
++[x]
++ quicksort[z | z <- xs; z>=x]
Läs så här:
En del tips finns.
1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, ....Primtalen kommer "ibland" parvis
<3,5>, <5,7>, <11,13>, <17,19>, <29,31> ...Skriv en funktion som genererar denna (möjligtvis?) oändligt långa lista av tal. Ditt program ska använda algoritmen Erathosetenes såll, som återfinns i läroböcker i algebra.
INTRODUCTION Standard ML is a statically scoped interactive functional language with a polymorphic static type system, polymorphic references, polymorphic exceptions, a sophisticated modules system and a formal semantics. The ML project won the British Computer Society's Technical Award for 1987. It is a general purpose programming language which is currently used for formal verification, VLSI work, microprocessor design, graphical interfaces, and compilers. THE DEFINITION. Robin Milner, Mads Tofte and Robert Harper The Definition of Standard ML MIT, 1990. Robin Milner and Mads Tofte have written a commentary on the Definition, which is being published by MIT. TEXTS. The first book is quite slow-paced and is aimed at people learning to program. It doesn't cover the modules system. Ake Wikstrom Functional Programming Using Standard ML Prentice Hall 1987 ISBN: 0-13-331661-0 The next book goes at a faster pace, and includes an introduction to the modules system. It also includes sections on denotational semantics, lambda calculus and implementation techniques. Chris Reade Elements of Functional Programming Addison-Wesley 1989 ISBN: 0-201-12915-9 The following report is available from the LFCS (Dorothy McKie, dam@ecsvax.ed.ac.uk) and costs 5 pounds or 10 US dollars. It covers all of Standard ML. Robert Harper Introduction to Standard ML LFCS Report Series ECS-LFCS-86-14 Laboratory for Foundations of Computer Science Department of Computer Science University of Edinburgh Nov. 1986 (revised Jan. 1989 by Nick Rothwell and Kevin Mitchell) The following report is available from the LFCS (Dorothy McKie, dam@ecsvax.ed.ac.uk) and is free. It includes an introduction to Standard ML and three lectures on the modules system. Mads Tofte Four Lectures on Standard ML LFCS Report Series ECS-LFCS-89-73 Laboratory for Foundations of Computer Science Department of Computer Science University of Edinburgh March 1989 The following report is available from the LFCS (Dorothy McKie, dam@ecsvax.ed.ac.uk) and is free. It introduces Extended ML, a language for writing (non-executable) specifications of Standard ML programs and for formally developing Standard ML programs from such specifications. Don Sannella Formal program development in Extended ML for the working programmer. LFCS Report Series ECS-LFCS-89-102 Laboratory for Foundations of Computer Science Department of Computer Science University of Edinburgh December 1989 Larry Paulson and Stefan Sokolowski both have books on Standard ML in preparation.Åke Wikströms bok finns i kursbiblioteket.
1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, ....Primtalen kommer "ibland" parvis
<3,5>, <5,7>, <11,13>, <17,19>, <29,31> ...Skriv en funktion som givet ett naturligt tal, n, genererar de n första primtalsparen. Ditt program ska använda algoritmen Erathosetenes såll, som återfinns i läroböcker i algebra.
DEF Subset AS distl | EACH member END | and;
Läs ungefär så här i ett exempel "anrop" exempel:
show
<<4,2,5,1,3> <1,2,3>> : Subset
Distribuera den ena listans element över den andra:
<<<4,2,5,1,3>,1 > <<4,2,5,1,3>2,> <<4,2,5,1,3>3,>> : EACH member END | and
Applicera medlem på varje på så sätt producerat par <lista, element>:
< T, T, T> : and
Applicera and
på alla element i den skapade listan:
T
En del tips finns.
Båda i kursbiblioteket.
Du bör under din lektion välja att hålla dig till en syntax, exvis IFP, men du ska även prata om grundläggande idéer, exvis från Bacchus artikel.
Simulatorn skall vara distribuerad på minst två olika maskiner.
Exempel
Användarsnittet i en Lisp-interpretator kan beskrivas så här
(do forever (print (eval (read))))där eval tar en programspråkskonstruktion i Lisp och returnerar värdet av denna. Idé om hur eval kan se ut
(defun eval (e env)
(cond ((isconst e) (denote e)
((isvar e) (lookup e env))
((iscond e)
(evcond (arg e) env))
((isquote e) (dequote e))
((isfunc+arg e)
(apply (func e)
(evalarg (arglist e)
env)
env))))
där
apply applicerar en funktion på utvärderade argument
evalarg utvärderar argument
eller
eller
Darlington m.fl., Functional Programming and its Applications, kap "Interpreters for Functional Languages", s 253. Boken kan lånas för kopiering.
Anders Berglund Office: Room 1254
Department of Computer Systems E-mail: Anders.Berglund@docs.uu.se
Box 325 Phone (work): +46 18 471 31 67
S-751 05 Uppsala Mobile phone: +46 70 582 45 80
Sweden Fax (work): +46 18 55 02 25
Senast ändrad: 09/21/98