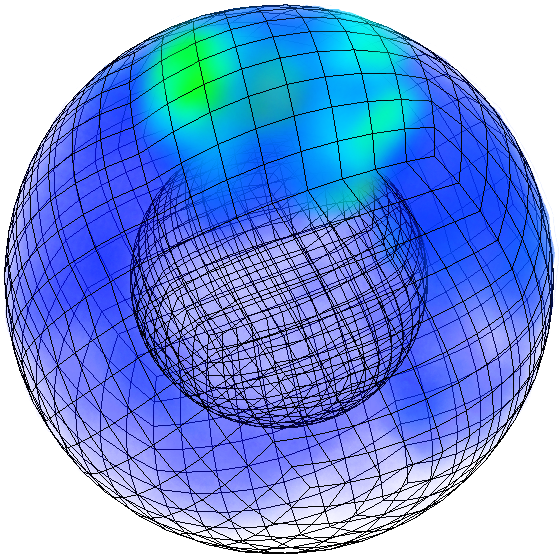
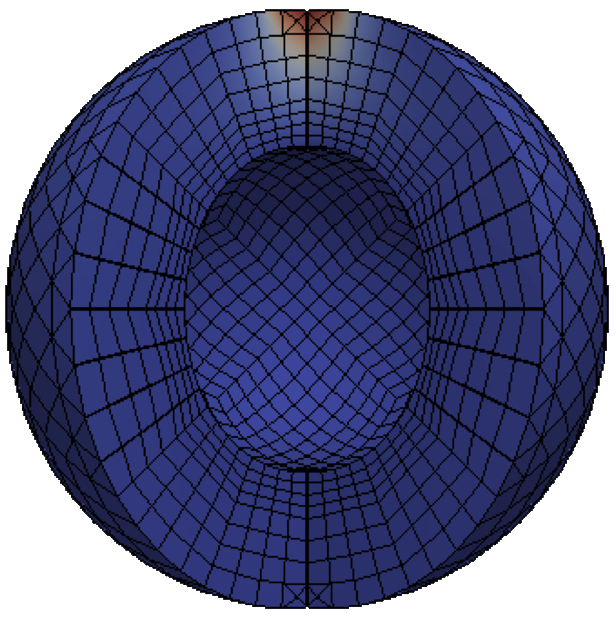
Glacial Isostatic Adjustment (GIA) describes the response of the solid Earth to redistribution of surface loads due to the growth or decay of large ice masses. Ice advance and recession, as well as the recent global warming trend, induce sea-level changes and migration of coast lines. The effect GIA processes has on human life has attracted researchers to this field. During glaciation, the ice is built up on the surface. The increasing load cause subsidence of the earth surface into the mantle. When the process of deglaciation starts, the earth rebounds reversing the subsidence process. GIA process described above is time dependent due to the viscoelastic properties of the Earth and involves time scales of 100000 years.
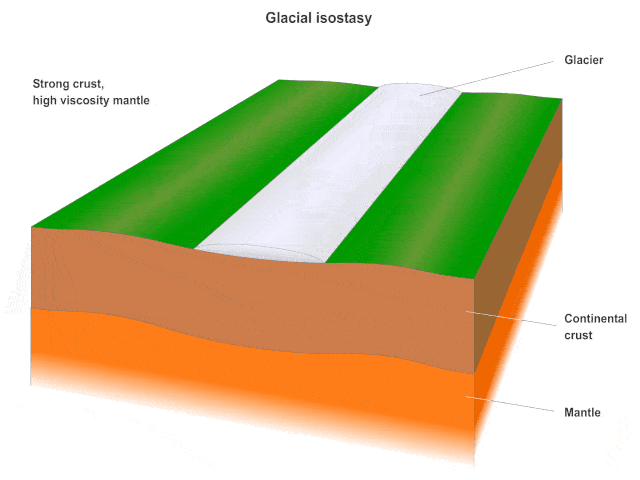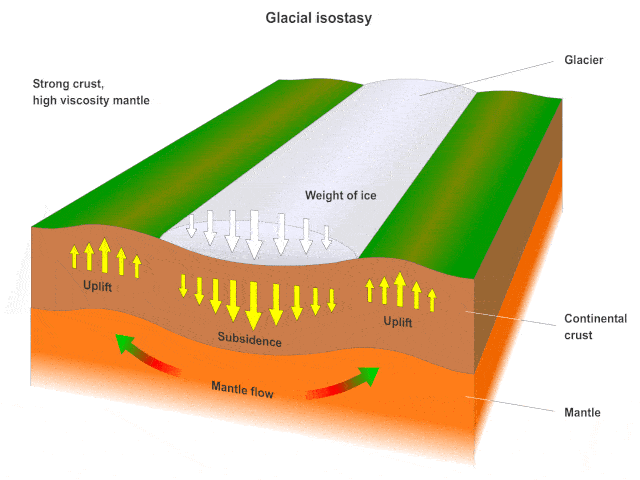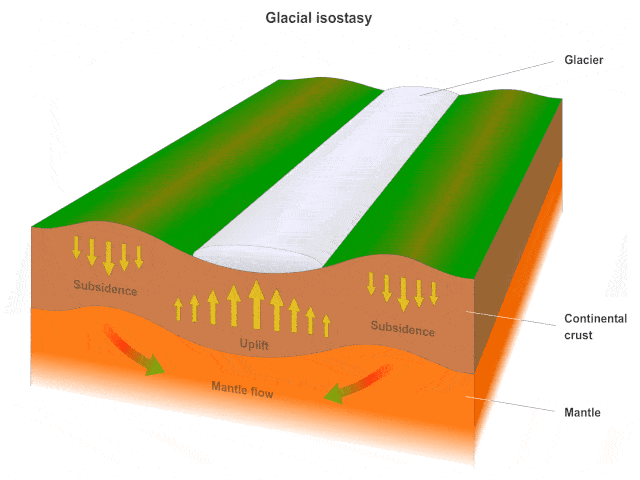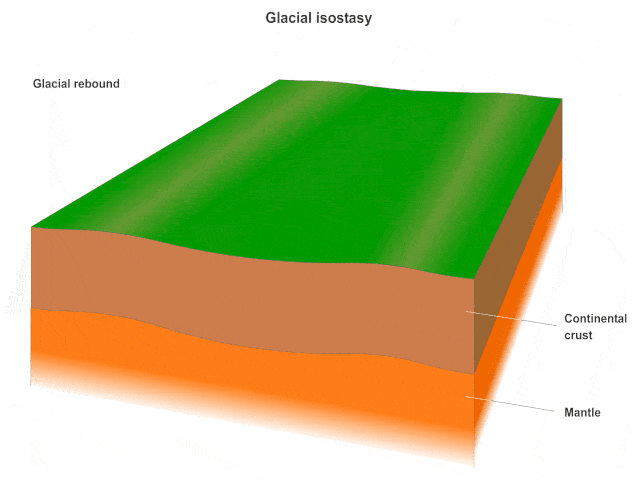
A lot of information can be deduced about ice history of the Earth from GIA models. Additionally, the study results of GIA can be used in atmosphere modeling to better describe the past climate changes as well as global warming and future trends. Moreover, the study of the change in the surface pressure may provide invaluable information on understanding volcanic activities and earthquakes. This in turn may be used in determining a place for nuclear waste which is safe for thousands of years. GIA is also a primary cause of long-term Earth rotation variability.
The complexity and the enormous space and time scales of the GIA model leave computer simulations as the only viable option to study GIA phenomena. However, until recently, most simulations have been carried out on 2D geometries with simplified models. On the other hand, new studies have shown the need to model complex geometries and 3D Earth structures in order to explain the past ice trends. The above mentioned complexities has prompted an interest to use the finite element method (FEM).
Currently, no publicly available FEM codes implements the main GIA complexities; commercial codes are used with inappropriate description of the physics.
This project aims at tackling the many challenges of correctly simulating gia model in full complexity. our ambition is to provide accurate and efficient computer simulation tools for glacial isostatic adjustment (GIA) models.
This project will develop and analyse FEM-based methods to simulate a more complete description of the GIA process, allowing accurate simulations of complex 3D models with material inhomogeneities. Novel robust and scalable numerical solvers will be developed, including optimal order preconditioned iterative methods. The outcome, a freely available, accurate and efficient simulation code will be a valuable tool box for the GIA community and will enable better understanding of the GIA process in regions with laterally varying Earth properties, such as Iceland.
The driving force for the project is the need to address applied problems of very high complexity, the solution of which is of utmost importance for our society. Such problems are characterized by complicacy, heterogeneity, mutual dependencies, unknown parameters and large space and time domains, that preclude analytical approaches and promote numerical simulations as the only feasible way to approximate the solution.
As the main reference application we consider the GIA processes. In mathematical terms these processes are described by a coupled system of integro-differential equations that have to be discretized appropriately and accurately enough, and solved using efficient numerical solution methods that are robust with respect to problem, discretization and method parameters.
Accuracy, robustness and efficiency in terms of computational cost are to be achieved answering the following major questions with mathematical rigor:
Moreover, the computational power and the memory resources needed for the GIA simulation is extremely high which introduces another aspect to this research. Thus, the implemented methods are needed to be robust, accurate and numerically efficient. At the same time, the implementations should also be highly parallel and memory efficient to best utilize the available computer resources and be a feasible method to simulating GIA model.
Currently we have developed the 2D elastic model. The benefits of this are twofolds; firstly, the elastic response of the earth is the building block for the simulation of the viscoelastic materials; Secondly, the acquired results can be compared against the available 2D implementation to test the correctness. The 2D implementation has been tested on clusters and has been shown to be very efficient both numerically and computationally. Moreover, the spectral properties of the used preconditioner is analysed to show the quality of the preconditioning method(See List of publication for details). The figure below shows the simulation on a half space homogeneous Earth with a load on the top left boundary.
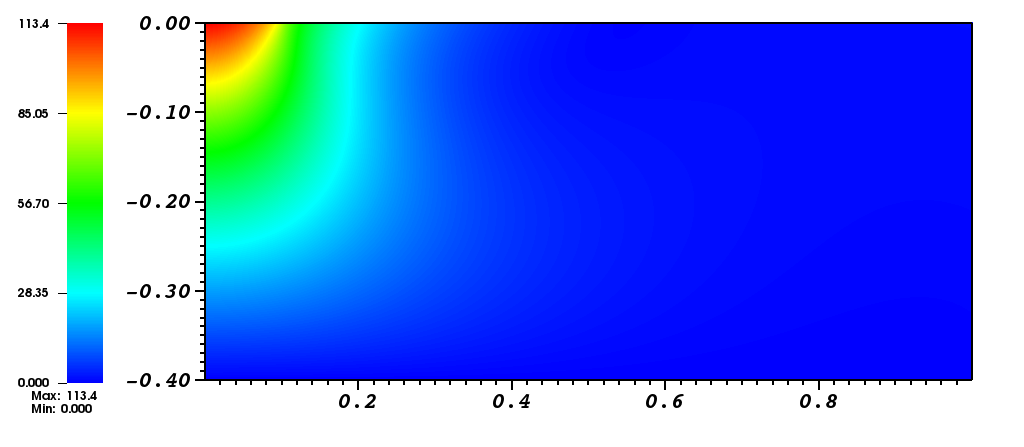
Furthermore, the 3D elastic problem is implemented and is in the optimization process. Some preliminary results are presented below which are studied for further improving the overall performance of the method (numerical and computational).
| #DOF | Iteration | Time | ||||
| outer | Inverse | Schur | Assembly | Prec. Setup | Solve | |
| 21760 | 9 | 5 | 1 | 2.1 | 0.687 | 26.2 |
| 163704 | 9 | 1 | 1 | 17.1 | 4.8 | 164.77 |
Maya Neytcheva is a senior lecturer at the IT department of Uppsala university
Björn Lund is a senior lecturer at Devision of Earth Sciences, Geophysics, Uppsala University.
Ali Dorostkar is a PhD student in Uppsala University. His supervisors are
Maya Neytcheva ,
Björn Lund
and
Lina Von Sydow.
Thora Árnadóttir
is a research professor at the Nordic Volcanological Center, Institute of Earth Sciences
Stefano Serra-Capizzano is a full Professor in Numerical Analysis and
the director of the Department of Physics and Mathematics,
Insubria university, Italy.